Simulated Annealing

단원

Combinatorial Optimization

1. 정의

Data: Baseball Salaries

기본 셋팅

Code

•

최적해 Update에 관한 내용이 나오기 때문에 Fixed-Point Iteration 나 Newton-Raphson Method 을 먼저 확인하고 오시는 것이 좋습니다.

1. 정의

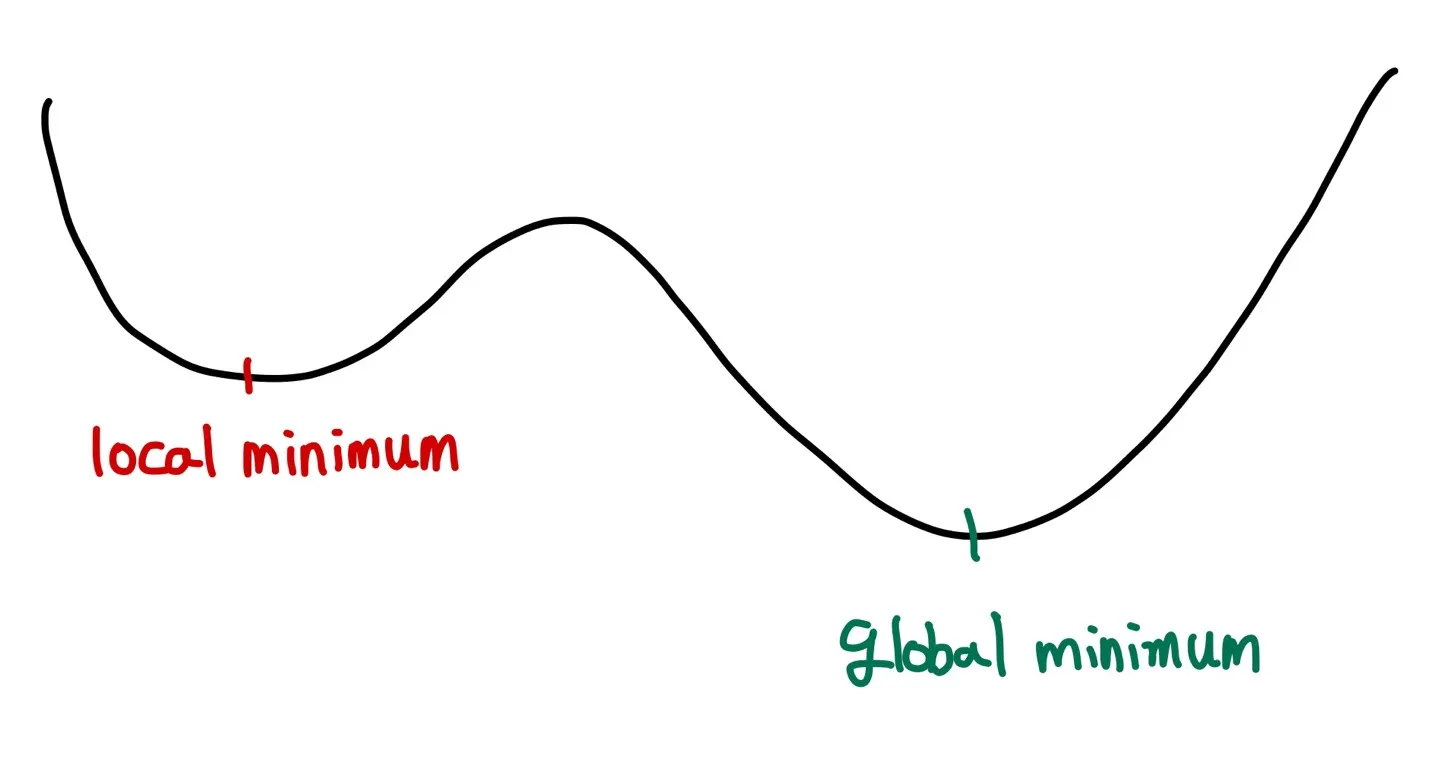
담금질 기법(Simulated Annealing)은 전역 최적화(global optimization) 방법 중에 하나로, 우리가 발견해낸 값을 점진적으로 최적점 또는 해에 가깝게 계속해서 update 하되, 적은 확률로 아주 먼 값으로 update를 하는 기법이다.

fixed-point iteration, newton-raphson method 같은 방법들의 문제점은 global minum(또는 maximum)이 아니라 local minimum(또는 maximum)에 빠질 위험이 있다는 것이었다. 그림을 통해 살펴보자.

fixed-point iteration이나 newton-raphson method는 minimum 값을 찾기 위해 기울기가 0이 되는 지점을 찾아갈 것이다. 그러나 문제는 local minimum을 찾으면 거기서 알고리즘이 멈추기 때문에 우리가 원하는 global minimum 값은 도달하지 못하게 된다. Simulated Annealing은 이러한 문제를 해결하기 위해 낮은 확률로 값을 튀도록 만들어준다. 여기서 튄다는 말은 값을 조금 멀리 보낸다는 뜻이다. 계속해서 그림을 통해 무슨 말인지 알아보자.

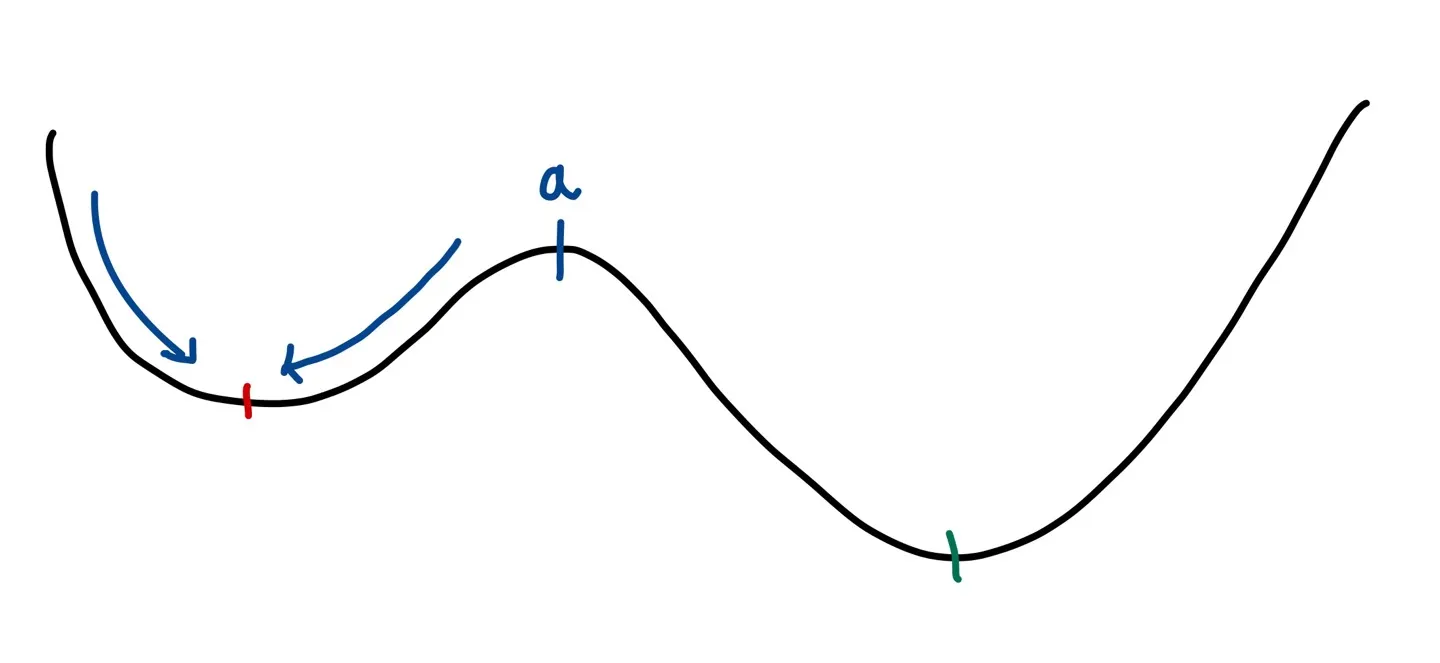
우선 시작점(starting point)이 a 지점보다 왼쪽에 있다고 하면(여기서 왼쪽 골짜기에 있다고 표현해보자) 우리는 계속해서 더 작은 값을 찾아갈 것이기 때문에 local minimum(빨간색 지점)을 향해 값을 update를 할 것이다.

즉 만약 a의 왼쪽에서 update를 시작하면 local minimum에 빠질 수밖에 없는 것이다. 그렇다면 우리는 a의 오른쪽(오른쪽 골짜기)에서 update를 진행해야 된다는 것을 알 수 있다. 그런데, 운 좋게 a의 오른쪽을 시작점으로 둔다면 global minimum을 찾아갈 수 있겠지만, 실제로 우리는 그래프의 모양을 알 수 없기 때문에 보통은 random하게 update의 시작점을 잡는다. 그래서 simulated annealing에서는 다음의 두 가지 방식으로 문제를 해결한다.

update의 후보값(candidate value)을 제시한다.

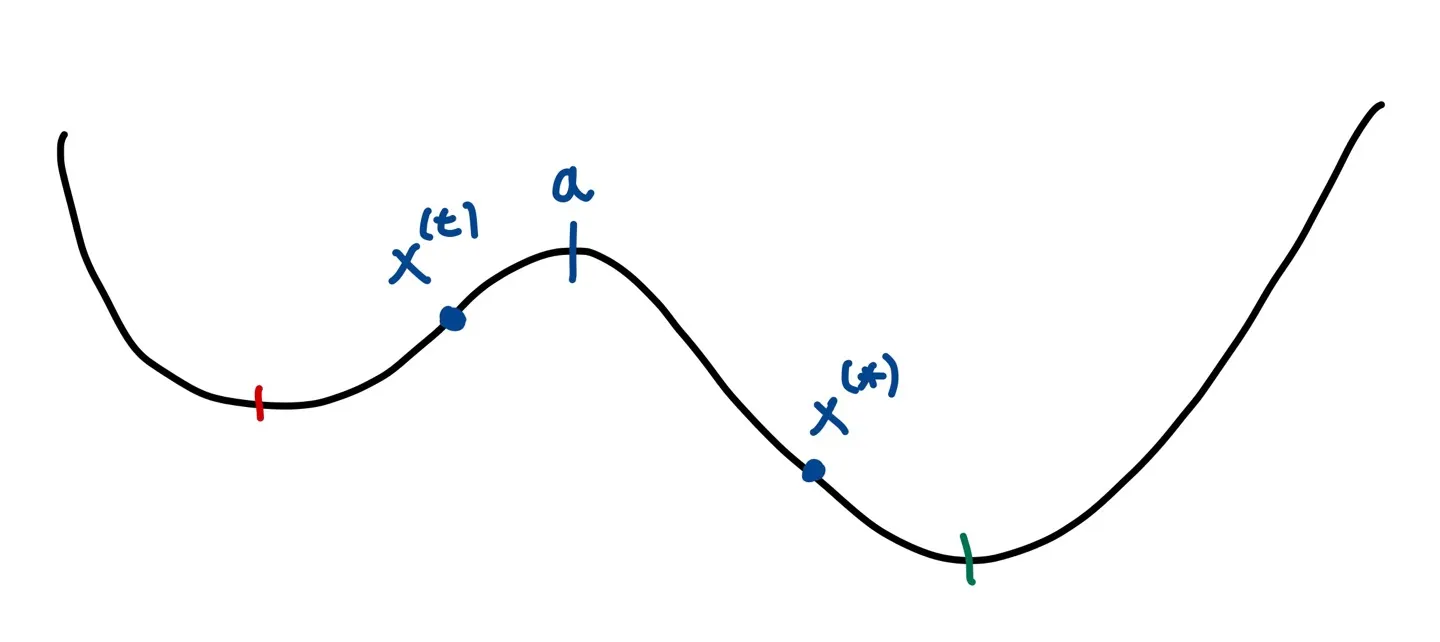
기존에 fixed-point iteration이나 newton-raphson 방식들은 update equation을 활용하여 최적값을 찾아갔다. 즉, 무조건 update되는 값이 정해져있는 방식이다. 그런데 simulated annealing에서는 update의 후보값을 설정한다. 즉, proposal density 등 특정한 방식(이는 뒤에서 좀 더 자세하게 설명할 것)으로 후보값을 제안하고 그 후보값이 update 조건에 맞으면 그 후보값을 채택하는 것이다. 이러한 방식은 우리의 updated value가 한쪽 골짜기에만 머무르는 것을 방지해준다.

위의 그림과 같이

x^{(t)}

에서 proposal density 등의 방법으로

x^{(*)}

의 값을 제안한다면, global minimum으로 도달할 수 있다.

함숫값이 더 작지 않더라도 특정한 확률로 후보값을 다음 update 값으로 채택한다.

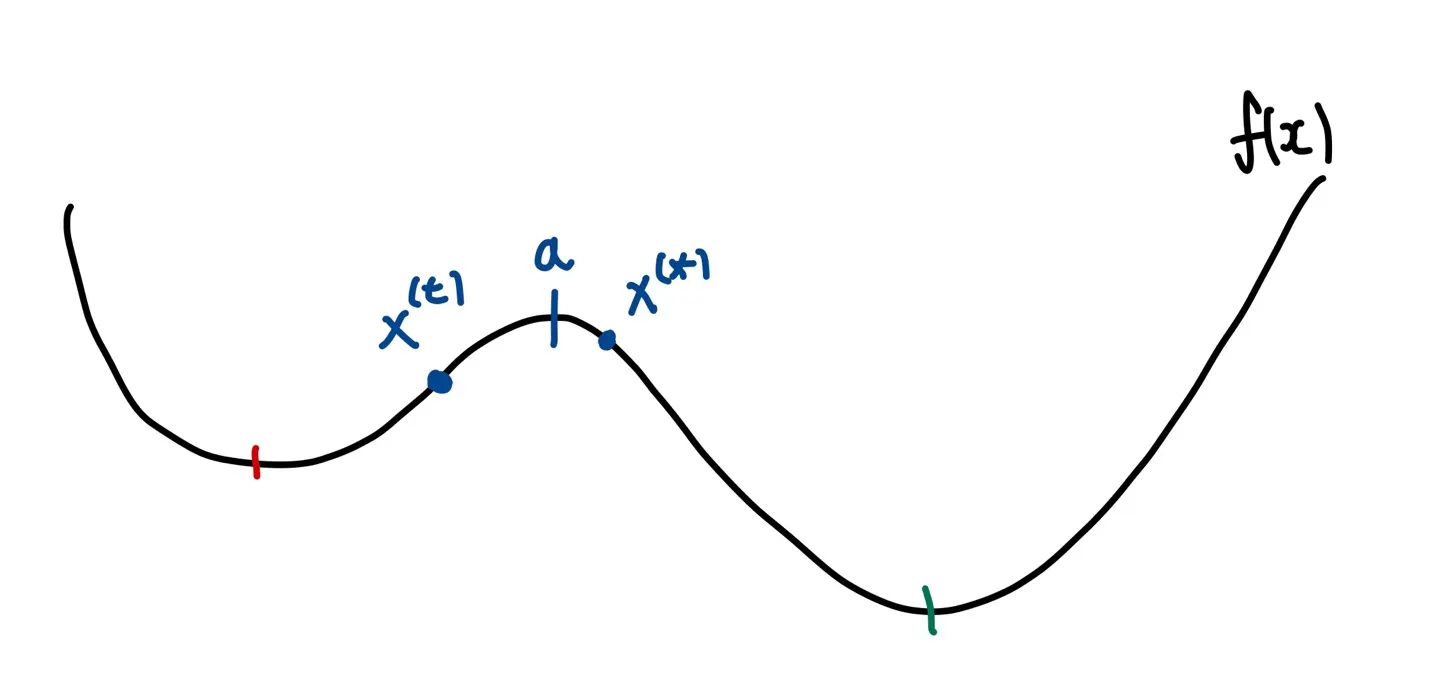
만약 함숫값이 더 작은 값들만 다음 update 값으로 채택된다고 하면 우리는 기껏 다른 골짜기에 후보값을 넣고도 채택을 안 할 수도 있다. 다음 예시를 살펴보자.

만약 위의 예시에서 함숫값이 더 작은 값만 다음 update 값으로 채택한다면,

f(x^{(t)}) < f(x^{(*)})

이기 때문에

x^{(*)}

는 global minimum의 골짜기에 포함되어있음에도 불구하고 다음 update 값으로 채택되지 않을 것이다. 따라서 우리는 비록 제시된 후보값의 함숫값이 기존의 값보다 더 높더라도 특정한 확률로 후보값을 채택하는 방식을 사용해야 한다.

2. Update Step

이번에는 좀 더 자세하게 update step을 살펴보자.

기본 설정

•

Update는 몇 개의 stage (j=0,1,2,...j=0,1,2,...j=0,1,2,...)로 구성되며 각 stage 안에 몇 번의 iteration으로 구성되어 있다. 각 stage를 cooling schedule이라고도 부른다.

•

Iteration의 인덱스는 ttt로 표현하며, t=0t=0t=0에서 시작한다.

•

시작점은 θ(0)\theta^{(0)}θ(0)이고 시작 온도(temperature)는 τ0\tau_0τ0​이다. 

•

온도(τ\tauτ)는 항상 양수이다.

•

θ\thetaθ는 iteration에 따라서 update 되며 온도는 각 스테이지에 따라서 update 된다. 즉, 같은 stage 내에서 온도는 동일하다.

•

각 stage에서의 iteration 수는 mjm_jmj​로 표현한다.

Iteration Step

다음의 step은

f(x)

의 global minimum을 찾는 과정이다. 만약

f(x)

의 global maximum을 찾고 싶다면

g(x) = -f(x)

인 함수를 설정하여

g(x)

의 global minimum을 찾으면 된다.

후보값(candiate solution) θ∗\theta^{*}θ∗를 θ(t)\theta^{(t)}θ(t)의 neighborhood(N(θ(t))\mathcal{N}(\theta^{(t)})N(θ(t))) 안에서 고른다. (이 때 후보값을 proposal density에서 제시할 수 있다. g(.∣θ(t))g(.|\theta^{(t)})g(.∣θ(t)))

예를 들어, proposal density를

N(\theta^{(t)},1)

이라고 하자. 그러면

\theta^* \sim N(\theta^{(t)},1)

θ∗\theta^*θ∗를 min⁡(1,exp⁡[{f(θ(t))−f(θ∗)}/τj])\min (1, \exp [\{f(\theta^{(t)}) - f(\theta^{*}) \}/\tau_j])min(1,exp[{f(θ(t))−f(θ∗)}/τj​]) 의 확률로 θ(t+1)\theta^{(t+1)}θ(t+1)로 채택한다. 만약, θ∗\theta^*θ∗가 채택되지 않는다면,  θ(t+1)=θ(t)\theta^{(t+1)} = \theta^{(t)}θ(t+1)=θ(t)

•

만약 f(θ(t))>f(θ∗)f(\theta^{(t)}) > f(\theta^{*})f(θ(t))>f(θ∗) 라면 min⁡(1,exp⁡[{f(θ(t))−f(θ∗)}/τj])\min (1, \exp [\{f(\theta^{(t)}) - f(\theta^{*}) \}/\tau_j])min(1,exp[{f(θ(t))−f(θ∗)}/τj​])는 언제나 1이기 때문에 무조건 θ∗\theta^*θ∗를 채택한다. (θ(t+1)=θ∗)\theta^{(t+1)}=\theta^*)θ(t+1)=θ∗)

Step 1,2를 총 mjm_jmj​번 반복한다.

j가 증가함에 따라, τj\tau_jτj​와 mjm_jmj​를 update 한다. τj=α(τj−1)\tau_j = \alpha(\tau_{j-1})τj​=α(τj−1​),  mj=β(mj−1)m_j = \beta(m_{j-1})mj​=β(mj−1​), 이 때 α\alphaα와 β\betaβ는 함수.

•

α\alphaα는 temperature를 점진적으로 0 방향으로 낮추는 함수여야 한다. ex) τj=0.9∗τj−1\tau_j = 0.9*\tau_{j-1}τj​=0.9∗τj−1​

•

mjm_{j}mj​ 는 j가 증가함에 따라 증가하는 것이 좋다. 왜냐하면 τ\tauτ가 낮아질수록, 함숫값이 더 높은 candidate를 채택할 확률이 더 낮아지기 때문이다. 이를 어느 정도 보완해주기 위하여 iteration 수를 늘려주는 것.

Step 1부터 다시 시작.

따라서 가능한 총 시행횟수는

m_j *j

번이다. 물론 convergence criterion을 설정하여 일정한 수치 이상으로 solution 값이 변하지 않으면 시행을 중단하도록 만들 수 있다.

3. 장단점

장점

•

응용할 수 있는 범위가 넓다.

•

가능한 최적의 해를 구할 수 있다.

단점

•

계산 시간이 매우 오래 걸릴 수 있다.

4. Code 및 활용

Simulated Annealing은 다양한 분야에서 활용될 수 있다. 예를 들어, MLE를 구함에 있어서 Likelihood 함수를 뒤집으면

(-L(\theta))

global minimum을 찾는 문제가 되기 때문에 simulated annealing을 활용할 수 있다.

최적의 조합 문제(Combinatorial Optimization)에서도 자주 활용된다. Regression 문제에서 최적의 변수 조합은 무엇일까?(Variable Selection). AIC를 기준으로 모델의 성능을 평가한다고 했을 때, 후보 변수가 총 n개인 경우, 모든 값을 비교하려면 AIC를

2^{n+1}-1

개 구해야 한다(변수가 n개일 때 가능한 조합은

2^{n+1}-1

개(intercept 고려, 독립변수가 아예 없는 경우 제외)이므로). 당장에 변수가 9개만 되어도 AIC를 무려 1023개 구해야 하는 것. 따라서 AIC의 global minimum을 찾는 문제로 Simulated Annealing을 적용한다면 좀 더 빠르게 문제를 해결할 수 있다. 좀 더 자세한 예시를 code와 함께 살펴보자.

Data: Baseball Salaries

•

337명의 야구선수에 대하여 그들의 1991년의 27개의 baseball performance statistics와 1992년의 salary 정보 데이터가 있다.

•

1991년도 27개의 baseball performance statistics를 predictor variable로, 1992년의 salary를 response variable로 설정하여 어떤 performance statistics들이 salary를 가장 잘 설명하는지를 밝혀내보자.

기본 셋팅

•

Cooling Schedule은 총 15 stage로 구성한다.

•

첫 다섯 stage의 iteration의 길이는 60, 그 다음 다섯 stage의 iteration의 길이는 120, 마지막 다섯 stage의 길이는 220으로 설정한다.

•

α(τj−1)=0.9∗τj−1\alpha(\tau_{j-1}) = 0.9*\tau_{j-1}α(τj−1​)=0.9∗τj−1​

•

candidate solution 제시 방식: 27개의 predictor 중 랜덤으로 한 개를 골라서 만약 그 predictor가 θ(t−1)\theta^{(t-1)}θ(t−1)에 포함되어 있는 경우 제외하고, 포함되어 있지 않은 경우에는 포함시킨다. (flip)

•

평가 기준은 AIC로 한다.

Code

R을 사용하여 구현하였다.

## INITIAL VALUES
baseball.dat = read.table('baseball.dat',header=TRUE)
baseball.dat$freeagent = factor(baseball.dat$freeagent)
baseball.dat$arbitration = factor(baseball.dat$arbitration)
baseball.sub = baseball.dat[,-1] # Predictor variables
salary.log = log(baseball.dat$salary)
n = length(salary.log) # 총 인원
m = length(baseball.sub[1,]) # predictor variable 총 개수
cooling = c(rep(60,5),rep(120,5),rep(220,5)) #cooling schedule
tau.start = 10 #시작 온도
tau = rep(tau.start,15) # 온도
aics = NULL  #AIC


# INITIALIZES STARTING RUN, TEMPERATURE SCHEDULE
set.seed(1234)
run = rbinom(m,1,.5)
run.current = run
run.vars = baseball.sub[,run.current==1]
g = lm(salary.log~.,run.vars)
run.aic = extractAIC(g)[2] # AIC를 구함.
best.aic = run.aic
aics = run.aic #여기까지는 3.3과 동일
for(j in 2:15){tau[j] = 0.9*tau[j-1]} #온도가 이전의 0.9배로 줄어들도록 설정.


## MAIN
for(j in 1:15){

	# Model에서 더하거나 뺄 predictor를 랜덤으로 선택하고
	# 더 나은지 확인한다. 더 낫다면 선택.
	for(i in 1:cooling[j]){
		pos = sample(1:m,1) #독립변수 중 한 개를 랜덤으로 선택
		run.step = run.current
		run.step[pos] = !run.current[pos] #선택된 독립변수를 flip
		run.vars = baseball.sub[,run.step==1] #flip된 변수 적용
		g = lm(salary.log~.,run.vars)
		run.step.aic = extractAIC(g)[2]
		p = min(1,exp((run.aic-extractAIC(g)[2])/tau[j]))
		if(run.step.aic < run.aic){
			run.current = run.step
			run.aic = run.step.aic}
		if(rbinom(1,1,p)){ #만약 run.step.aic가 run.aic보다 크다면 p의 확률로 run.step을 채택
			run.current = run.step
			run.aic = run.step.aic}
		if(run.step.aic < best.aic){ 
		  #지금까지 나온 aic중 제일 작다면 best aic로 선택하고 best predictor subset으로 설정
			run = run.step
			best.aic = run.step.aic}
		aics = c(aics,run.aic)
	}
}

## OUTPUT
run 		# BEST LIST OF PREDICTORS FOUND
best.aic 	# AIC VALUE
R
복사

[1] 0 0 1 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0

[1] -416.214