Fixed-Point Iteration

단원

Optimization and Nonlinear Equations

1. 정의

1. 정의

고정점 반복법(Fixed-Point Iteration)은

f(x) = 0

을 만족하는

x

를 구하기 위해

x=g(x)

를 만족하는 함수

g

를 설정하여 해를 구하는 방법을 말한다. 이 때

x

를 함수

g

의 고정점(Fixed Point)이라고 부른다.

예를 들어,

f(x) = x-\cos x=0

이라 하자. 그러면 여기서 우리는 쉽게

x=\cos x = g(x)

로 함수

g

를 설정할 수 있다.

그런데, 위의 예시에서는

g

를 간단하게 구할 수 있는 형태로

f(x)

가 설정되어 있었지만,

f(x) = x^3+\cos x = 0

과 같이 단순하게 변형하기 힘든 경우도 있다. 이 때는 양변에

x

를 더해주어서 해결하는 방법이 있다.

x = x^3+ \cos x + x = g(x)

2. 계산

그럼 이 때 우리가 해야될 것은 고정점(fixed point)이 무엇인지를 밝혀내는 것이다. 고정점을 찾는 가장 간단한 방법은 업데이트 공식(Updating Equation)을 활용하는 것이다. 고정점 반복법에서 업데이트 공식은 다음과 같다.

x^{(t+1)} = g(x^{(t)})

예를 들어, 시작점으로

x^{(1)} = 3

을 지정했다고 가정하자. 그러면

x^{(2)}=g(3)

이고

x^{(3)}=g(x^{(2)})

가 된다. 이렇게 반복적으로

x

를 업데이트하면

x=g(x)

를 만족하는 고정점에 근사할 수 있다.

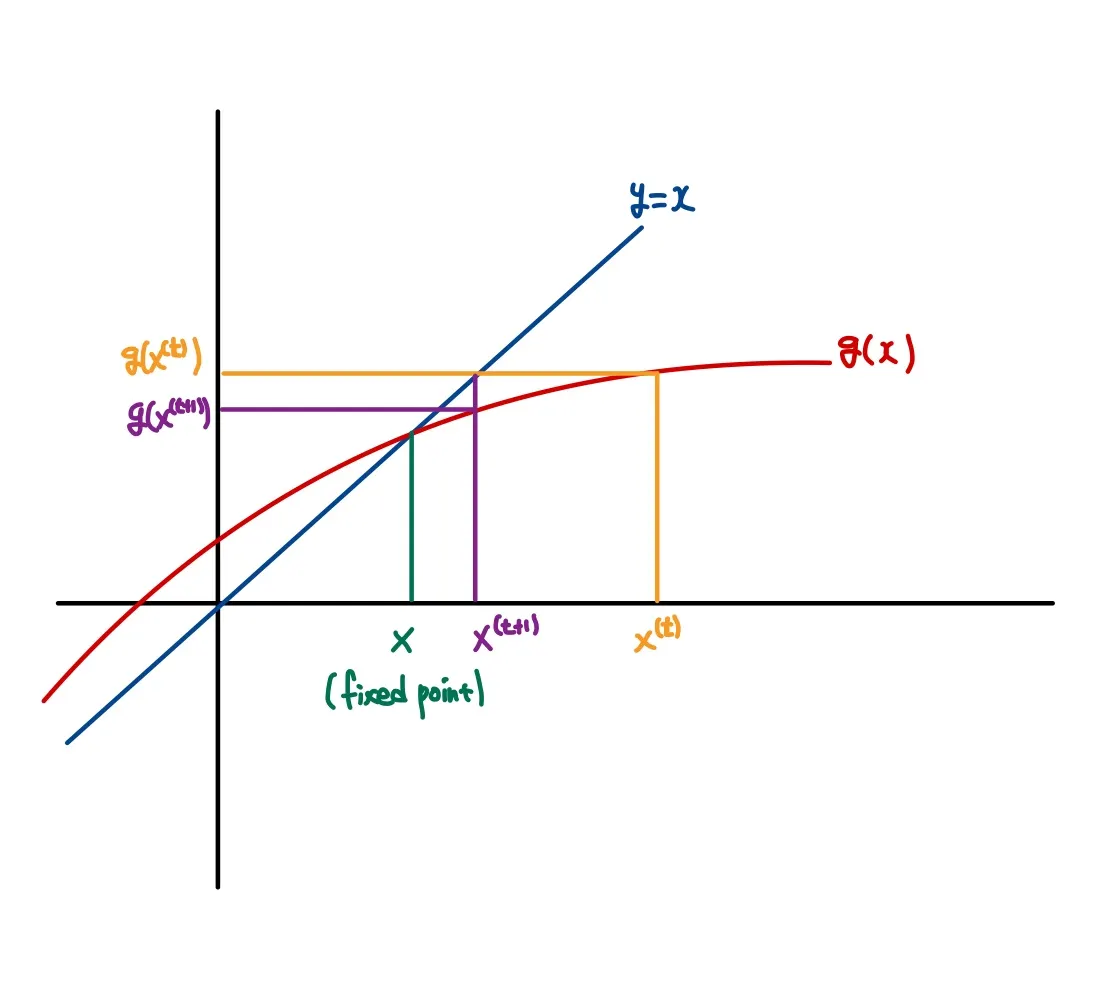
이 원리를 그림으로 이해하면 더 간단하다.

그리고 앞에서 양변에 x를 더했던 방법을 이용하여 다음의 업데이트 방정식을 구할 수 있다.

x^{(t+1)} = x^{(t)} + f(x^{(t)})

그런데 이 때

f'

이 bounded이고 정의역인 [a,b] 상에서 부호가 변하지 않는다면(does not change sign),

f(x)

대신

\alpha f(x)

를 사용할 수 있다(Scaling). 단,

\alpha \neq 0

3. 장단점

장점

•

이분법에 비하여 빠르다.

•

복잡한 상황에서도 사용 가능하다.

단점

•

적절한 함수 g(x)를 찾아야 한다.

•

Newton Raphson Method에 비해서 느리다.

4. Code

fixed-point iteration을 R코드로 구현하면 다음과 같다.

fixed_method <- function(f, start, alpha, tol = 1e-9, iter = 500){
  x <- start       # 시작점
  for(i in 1:iter){
    x_new <- alpha*f(x) + x      # 업데이트 방정식
    if(abs(x_new-x) < tol){
      return(x_new)
    }
    x <- x_new
  }
  return(x)
}
R
복사

5. 활용

다른 최적화 방법들과 마찬가지로 MLE 등 Maximum 값을 찾을 때 유용하게 사용된다.

다음의 함수가 최댓값을 가지는 지점을 fixed-point iteration 방법으로 찾아보자.

f(x) = \frac{\log (x)}{(x+1)}

우선

f(x)

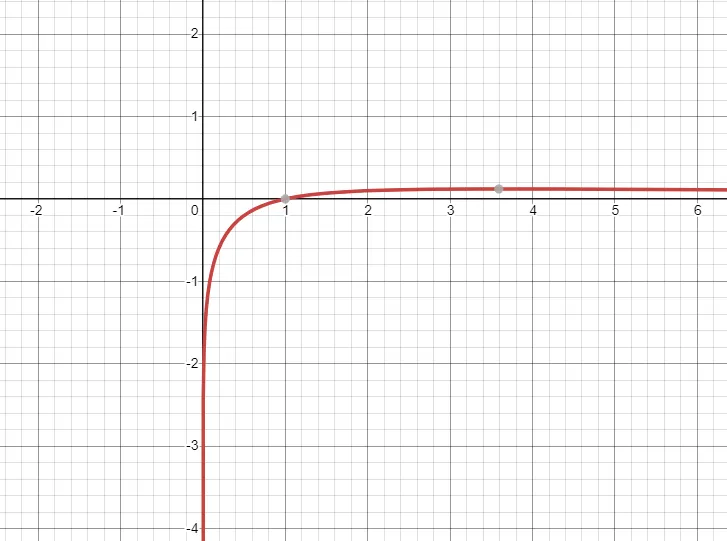
의 함수 그래프는 다음과 같은 모양이다.

3과 4 사이에 대략 최댓값을 가지는 지점이 존재하는 함수이다.

또한 위로 볼록한 형태의 연속 함수이므로 도함수가 0이 되는 지점을 찾으면 최댓값을 갖는 지점을 찾을 수 있다.

f(x)

의 도함수를

g(x)

라 하면

g(x)

는

g(x) = \frac{1}{x(x+1)}-\frac{\log x}{(x+1)^2}

이다.

g(x) =0

을 만족하는

x

를 fixed-point iteration으로 찾으면

fixed_method <- function(f, start, alpha, tol = 1e-9, iter = 500){
  x <- start
  for(i in 1:iter){
    x_new <- alpha*f(x) + x
    if(abs(x_new-x) < tol){
      return(x_new)
    }
    x <- x_new
  }
  return(x)
}

g <- function(x){
  res = 1/(x*(x+1)) - log(x)/((x+1)^2)
  return(res)
}

fixed_method(g, 2, 1, iter = 1000)
R
복사

3.591121

optimize function으로 최대 지점을 찾으면, 위의 결과와 동일함을 보인다.

f <- function(x){
  res = log(x)/(x+1)
  return(-res)
}

optimize(f, c(0,10))
R
복사

$minimum
[1] 3.591121