Newton-Raphson Method

단원

Optimization and Nonlinear Equations

1. 정의

1. 정의

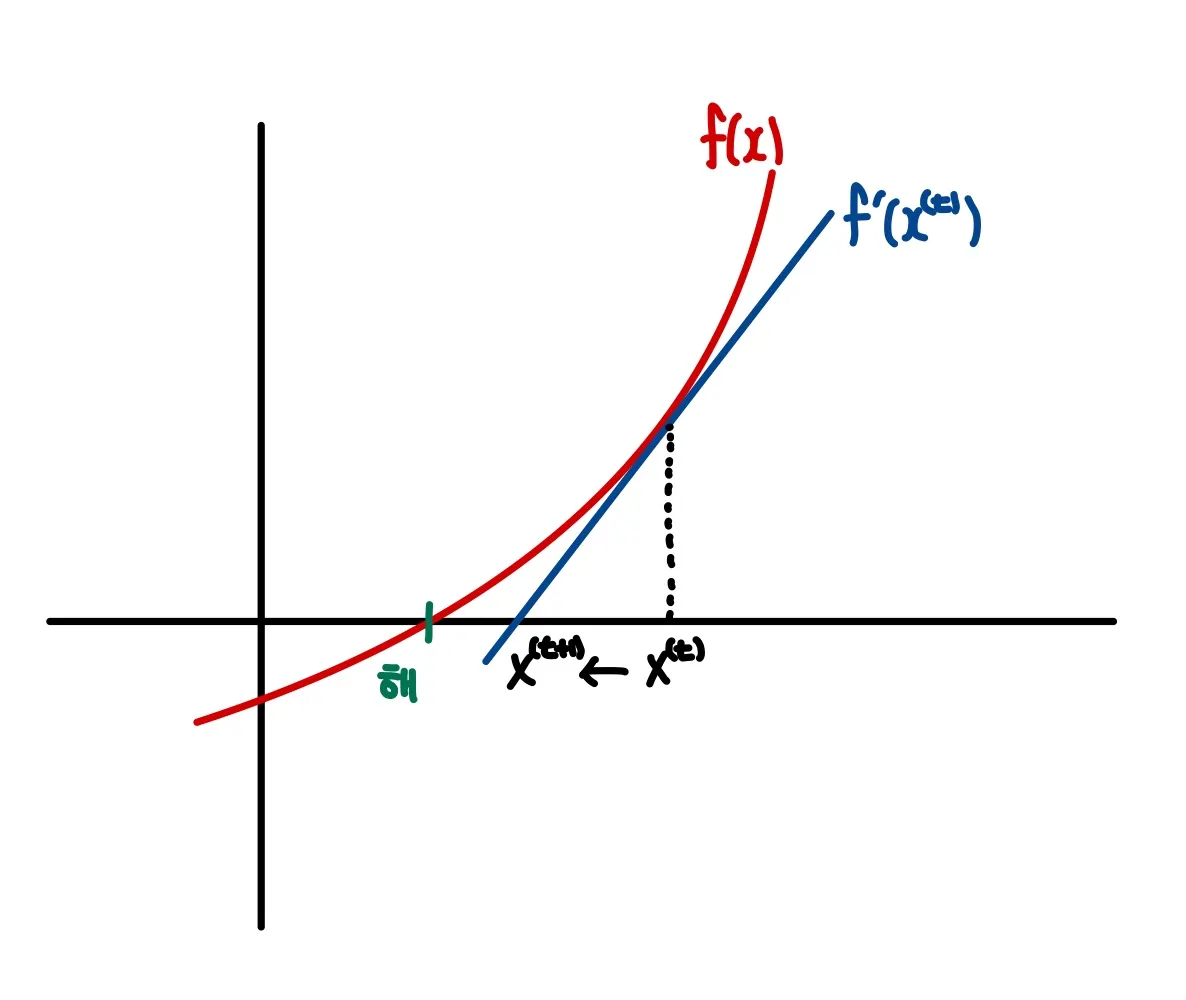
뉴턴-랩슨법(Newton-Raphson Method)는 현재 x값에서 접선을 그리고 접선이 x축과 만나는 지점으로 x를 계속 update하면서 점진적으로 해를 찾아가는 방법이다.

2. 계산

Fixed-point Iteration과 마찬가지로 Newton-Raphson Method는 updating equation이 존재한다.

x^{(t+1)} = x^{(t)}-\frac{f(x^{(t)})}{f'(x^{(t)})}

f(x^{(t)})

와

f'(x^{(t)})

의 부호의 경우의 수를 생각해보자.

f(x(t))>0,f′(x(t))>0f(x^{(t)}) >0, f'(x^{(t)})>0f(x(t))>0,f′(x(t))>0  또는 f(x(t))<0,f′(x(t))<0f(x^{(t)}) < 0, f'(x^{(t)}) < 0f(x(t))<0,f′(x(t))<0 

이 경우에 해는 현재

x^{(t)}

보다 왼쪽에 위치한다. 따라서 update 되는 값은

x^{(t)}

보다 작아야 한다. 그런데

f(x^{(t)}) *f'(x^{(t)})>0

이므로

x^{(t)}

에서

\frac{f(x^{(t)})}{f'(x^{(t)})}

를 빼면

x^{(t)}

보다 값이 작아진다.

f(x(t))<0,f′(x(t))>0f(x^{(t)}) < 0, f'(x^{(t)}) > 0f(x(t))<0,f′(x(t))>0  또는 f(x(t))>0,f′(x(t))<0f(x^{(t)}) >0, f'(x^{(t)})<0f(x(t))>0,f′(x(t))<0

이 경우에 해는 현재

x^{(t)}

보다 오른쪽에 위치한다. 따라서 update 되는 값은

x^{(t)}

보다 커야 한다. 그런데

f(x^{(t)})*f'(x^{(t)})<0

이므로

x^{(t)}

에서

\frac{f(x^{(t)})}{f'(x^{(t)})}

를 빼면

x^{(t)}

보다 값이 커진다.

그렇다면 왜 굳이

\frac{f(x^{(t)})}{f'(x^{(t)})}

를 빼는 것일까? 함수값의 절댓값이 작고 접선의 기울기가 가파른 경우를 상상해보자. 그러면 우리가 찾는 해는 지금의

x^{(t)}

값 근처에 위치할 것이다. 따라서 udpate 되는 값은

x^{(t)}

에서 큰 차이가 없어야 한다. 반대로 함수값의 절댓값이 크고 접선의 기울기가 완만하다면 우리가 찾는 해는

x^{(t)}

에 멀리 떨어진 곳에 위치할 것이다. 이때 update 되는 값은

x^{(t)}

에서 큰 차이가 있어야 한다. 따라서

x^{(t)}

에서

\frac{f(x^{(t)})}{f'(x^{(t)})}

를 빼주면 두 가지 경우를 모두 고려해 줄 수 있다. 그림을 그려보면 좀 더 이해가 쉬울 것이다.

Fixed-Point Iteration이나 Bisection Method와 마찬가지로 x 값에 변화가 거의 없을 때까지 계속해서 x를 업데이트한다. 그리고 오차가 기준값보다 작아지면 뉴튼-랩슨 법을 종료한다.

3. 장단점

장점

•

Fixed-point Iteration에 비하여 빠른 방법이다.

•

f’(x)f’(x)f’(x)를 구할 수 있다면 비교적 단순하게 update를 진행할 수 있다.

단점

•

f(x)f(x)f(x)가 정의역에서 연속이고 미분가능해야 한다.

•

해가 여러개인 경우 local optimum에 빠질 수 있다.

•

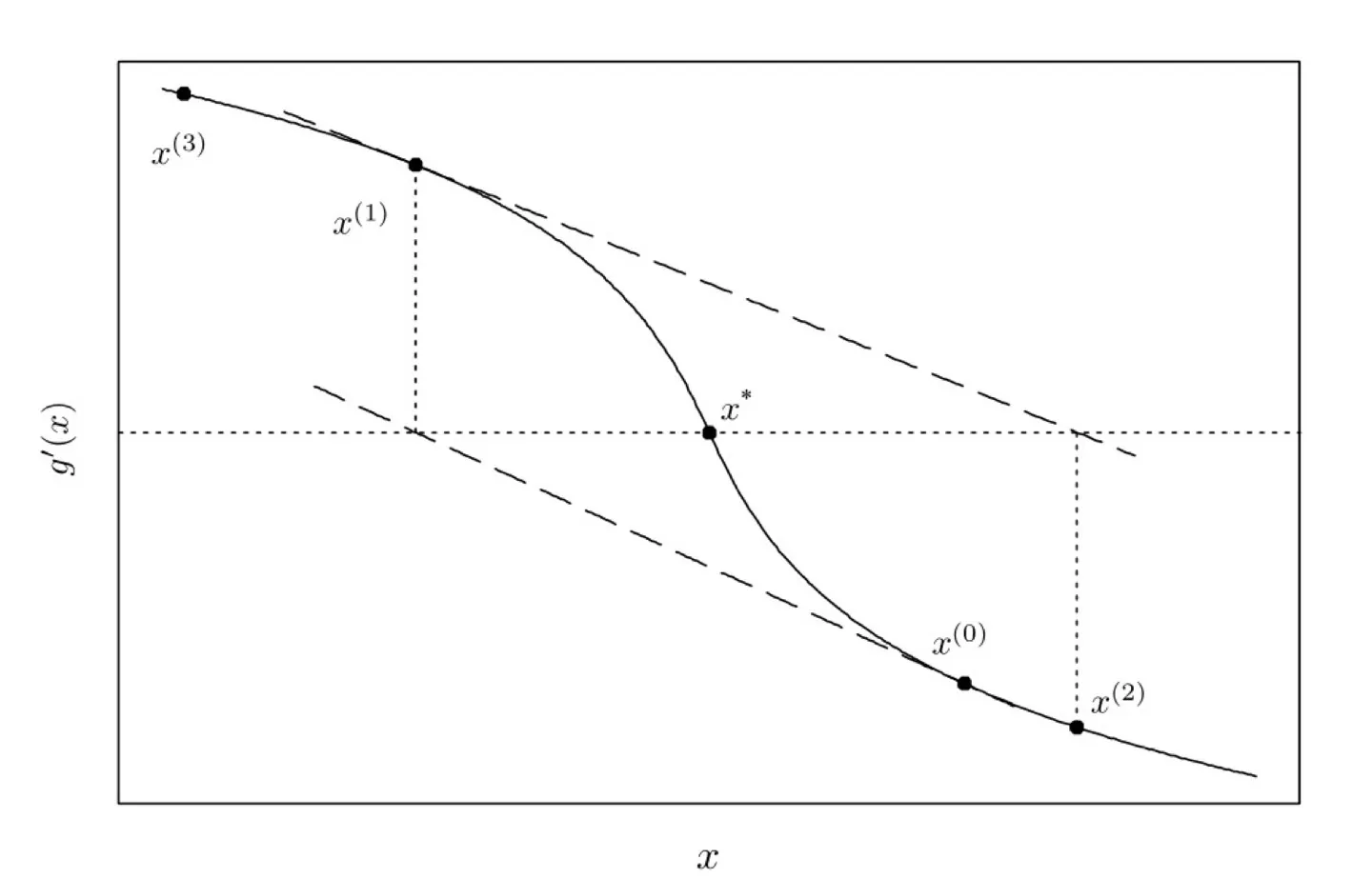
시작점에 따라선 x값이 converge하지 않고 끝날 수 있다.

ex)

4. Code 및 활용

코시 분포 평균 parameter의 MLE를 Newton-Raphson Method로 찾아보자.

기본 조건은 Bisection Method 의 5장과 동일하다.

이번에는 Rcpp로 코드를 구현해보았다.

// [[Rcpp::depends(RcppArmadillo)]]

#include <RcppArmadillo.h>
using namespace arma;

double gprime1(const double x, arma::dvec data){
  double value;
  value = 2*sum((data-x)/(1+arma::pow((data-x),2)));
  return value;
}

double gprime2(const double x, arma::dvec data){
  double value;
  value = 2*sum((arma::pow((data-x),2)-1)/arma::pow((1+arma::pow((data-x),2)),2));
  return value;
}

// [[Rcpp::export]]
double newton(double x, double epsilon, arma::dvec data, int max_iter){
  int i = 0;
  double diff = 1.0;
  
  while(fabs(diff) > epsilon){   // 오차가 epsilon보다 작아지면 탐색 중단.
    diff = -gprime1(x, data)/gprime2(x, data);
    x = x + diff;
    i = i + 1;
    if(i==max_iter){    // Converge하지 않을 수 있기 때문에 최대 iteration 수를 지정.
      cout << "Iteration is over. Need more max_iter. \n"<<endl;
      break;
    }
  }
  
  return x;
}
C++
복사

그리고 위의 코드를 cpp 파일로 저장하고, newton 함수를 R로 불러와서 MLE를 구해보자.

library(Rcpp)
library(RcppArmadillo)
sourceCpp("q2-1.cpp")

data <- c(1.77, -0.23, 2.76, 3.8, 3.47, 56.75, -1.34, 4.24, -2.44, 3.29,
            3.71, -2.4, 4.53, -0.07, -1.05, -13.87, -2.53, -1.75, 0.27, 43.21)

newton_list <- c(-11, -1, 0, 1.5, 4, 4.7, 7, 8, 38)   # 여러 시작점을 비교해보자.
for(i in newton_list){
  print(newton(i, 0.0001, data, 10000))
}
R
복사

[1] NaN
[1] -0.1922866
[1] -0.1922866
[1] 1.713587
[1] 2.817472
[1] -0.1922866
[1] 41.04085
[1] NaN
[1] 42.79538

→ MLE 값은 원래 약 -0.1922이다. 시작점에 따라서 MLE를 찾기도 하고 다른 값을 출력하기도 하고, 또 아예 값이 안 나오는 경우도 있다. 즉, newton-raphson 방법은 starting point에 의존한다는 것을 보여준다.