목차
1. 정의
이분법(bisection method)는 근이 반드시 존재하는 폐구간을 이분(bisect)한 후, 이 중 근이 존재하는 하위폐구간을 선택하는 것을 반복해서 근을 찾는 알고리즘이다. 말로 하면 복잡한데, 예시를 보면 조금 더 간단하다.
2. 계산
다음의 그림들을 통해 이분법 계산 순서를 살펴보자.
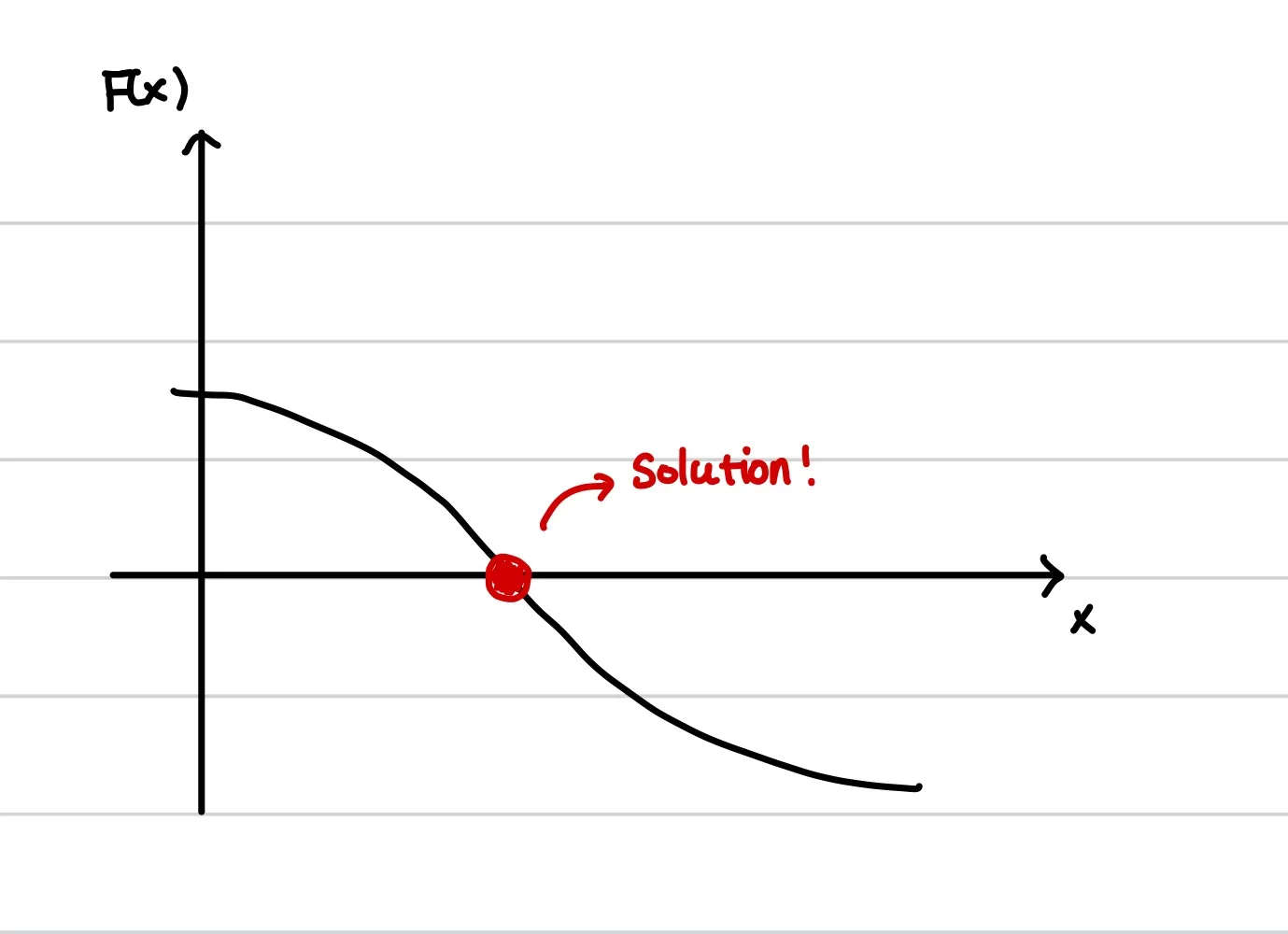
1.
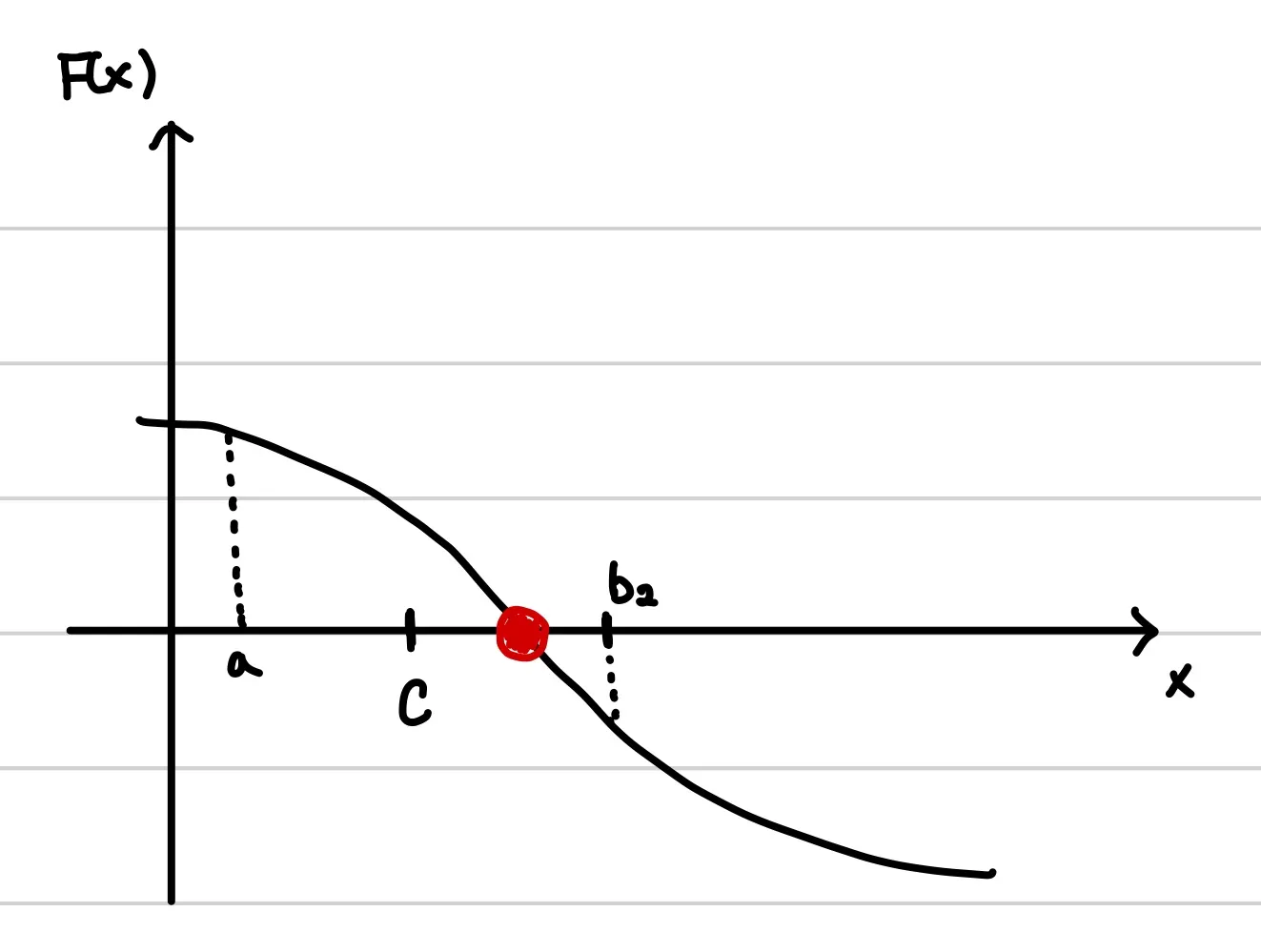
우선 이분법은 근이 반드시 존재한다고 가정한다. 따라서 정확히 어떤 값인지는 모르겠지만 다음과 같이 해가 존재한다는 것을 알고있다고 하자.
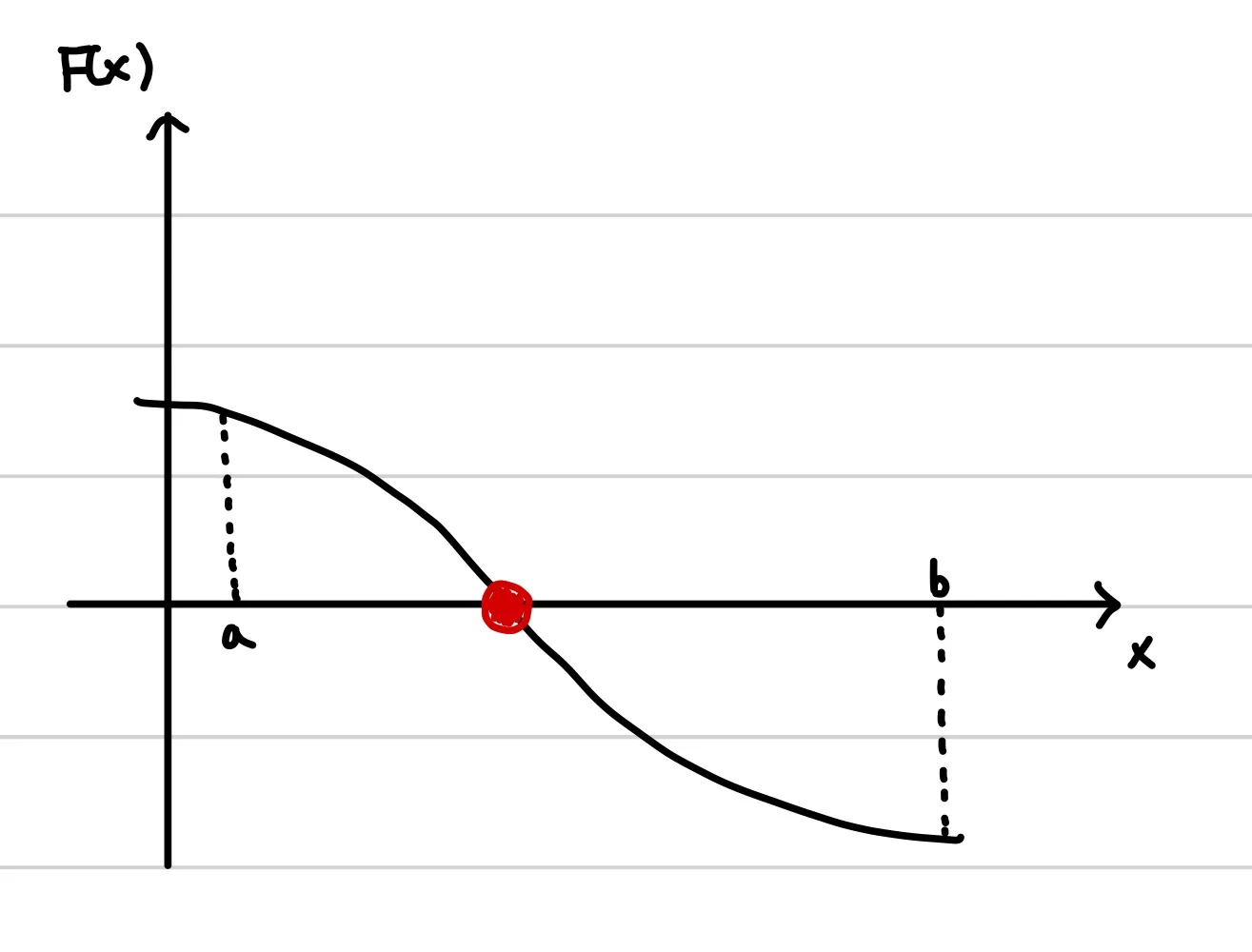
2.
다음으로는 해를 포함하는 폐구간을 설정한다. 물론 위의 그림에서는 우리가 함수의 모양을 알고 있기 때문에 폐구간을 설정하는 것이 쉽지만, 함수의 모양을 정확히 모르는 경우에는 폐구간을 잡는 것이 쉽지 않을 수 있다.
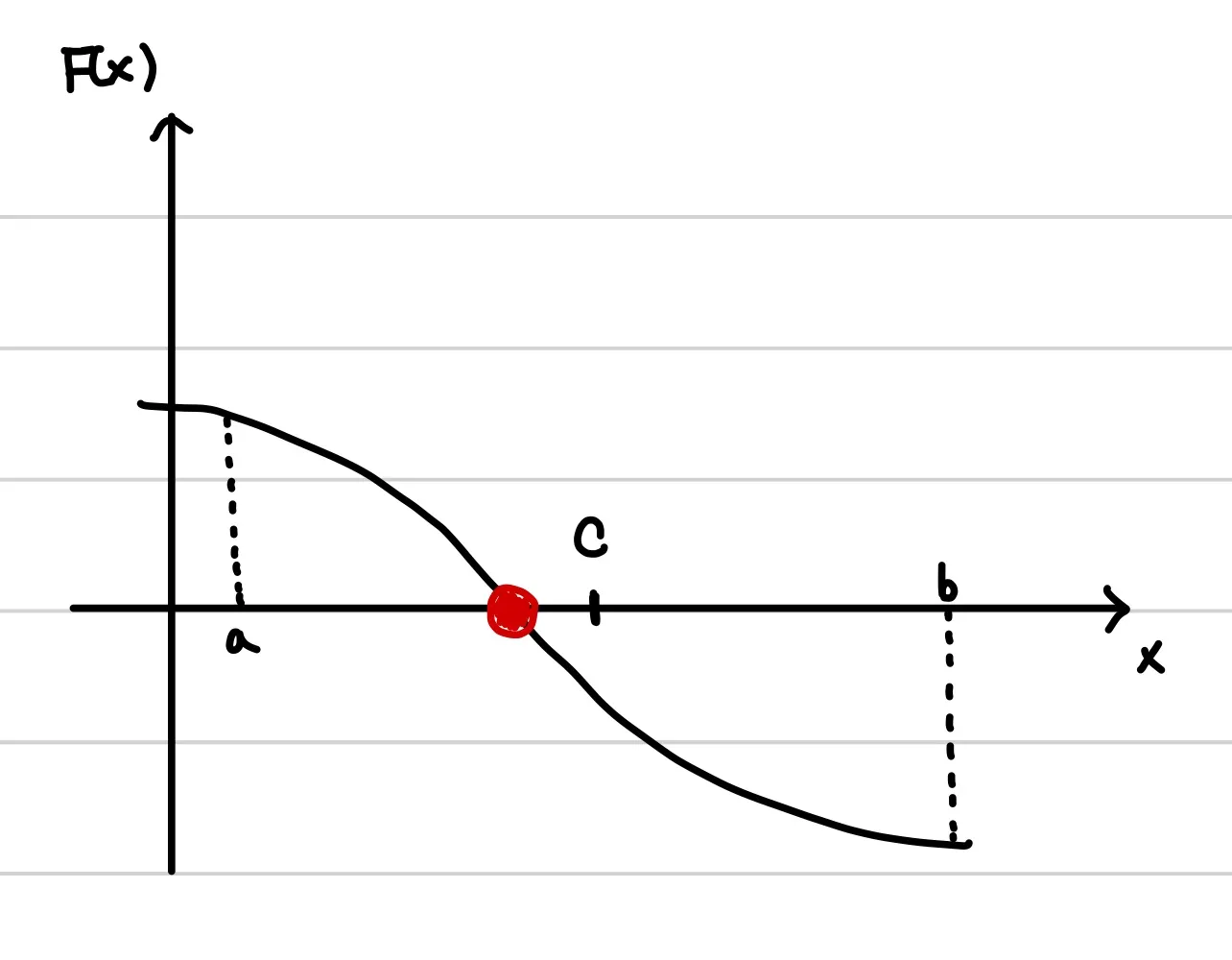
3. 다음은 폐구간 사이의 어느 한 점을 잡는다. 보통은 a와 b의 중간지점( (a+b)/2 ) 으로 잡는다.
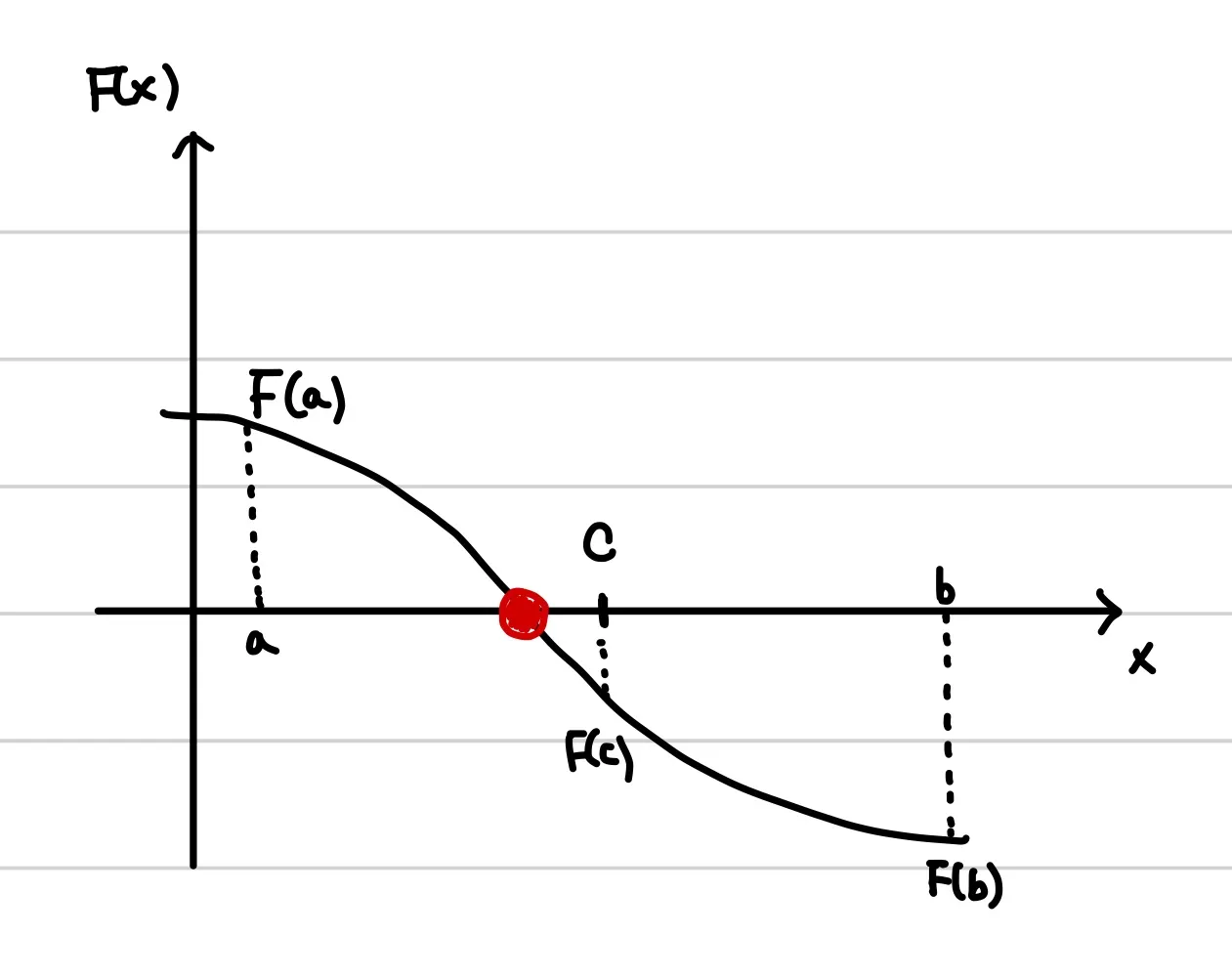
4.
이제 F(a)*F(c)와 F(c)*F(b)를 계산한다.
이 때 가능한 Case는 세 가지이다.
1) F(a)*F(c) > 0 (⇔ F(b)*F(c) < 0)
2) F(b)*F(c) > 0 (⇔ F(a)*F(c) < 0)
3) F(a)*F(b)*F(c) = 0 (⇔ F(c) = 0)
→ 1)은 c를 기준으로 해가 더 오른쪽에 위치하는 경우이다. 따라서 우리는 탐색 범위를 b와 c 사이로 재설정 해주어야 한다.
→ 2)는 c를 기준으로 해가 더 왼쪽에 위치하는 경우이다. 따라서 우리는 탐색 범위를 a와 c사이로 재설정 해주어야 한다.
→ 3)은 해를 찾은 경우로 탐색을 중단한다.
위의 예시에서는 F(b)*F(c) > 0 이므로 c를 b_2로 재설정해서 탐색범위를 왼쪽으로 옮겨주어야 한다.
5.
c를 b_2로 재설정하고 step1~4를 다시 반복한다.
그런데 일반적으로 정확한 해를 찾기는 쉽지 않다. 즉, F(c) = 0인 c를 찾는 것은 어렵다. 따라서 용인할 수 있는 수준인 threshold()를 설정해서 다음을 만족하면 탐색을 중단한다.
•
또는
•
또는
•
3. 장단점
장점
•
매우 간단한 방법이다.
•
해의 대략적인 위치를 안다면 일정 오차 내에 있는 해는 무조건 도출 가능하다.
단점
•
다른 해 찾기 방식들에 비해 느리다.
•
근이 존재한다는 점이 전제되어야 한다.
•
해의 대략적인 위치를 알아야 한다.
4. Code
# 함수 설정
bisect_func <- function(x){
2*(x/(1+x^2))
}
# setup
a = -1
b = 2
epsilon = 0.001
itr = 50
x = (a+b)/2
for (i in 1:itr){ # 최대 itr번만 수행한다.
if (abs(bisect_func(a)-bisect_func(b)) < epsilon){
break # 만약 |f(a) - f(b)| < epsilon 이라면 탐색 중단
}
if (bisect_func(a)*bisect_func(x) < 0) {b = x}
else if (bisect_func(b)*bisect_func(x) < 0) {a = x}
else break
x = (a+b)/2 # 값 새로 업데이트
}
x
R
복사
-6.103516e-05
→ 본래 함수의 해는 0이다. 0에 가까운 값을 찾은 것을 볼 수 있다.
5. 활용
이분법은 MLE(Maximum Likelihood Estimates)를 찾는 데에 활용할 수 있다. 만약 어떤 확률 모형 함수의 도함수를 알고있다고 가정하자. 만약 그 확률 모형 함수의 형태가 위로 볼록하거나 아니면 봉오리들을 가지고 있는 형태라면 MLE의 값을 도함수에 대입하면 0이 나올 것이다. 즉, MLE의 값은 도함수의 해이다. 따라서 도함수의 폐구간을 잡아서 이분법을 사용하면 MLE를 구할 수 있다.
예를 들어 우리가 어떤 값들이 cauchy 분포를 따르는 것을 알고 있지만, 그 코시 분포의 평균값은 모른다고 해보자. 우리가 가지고 있는 데이터는 다음과 같다.
mydata <- c(1.77, -0.23, 2.76, 3.8, 3.47, 56.75, -1.34, 4.24, -2.44, 3.29,
3.71, -2.4, 4.53, -0.07, -1.05, -13.87, -2.53, -1.75, 0.27, 43.21)
R
복사
평균이 인 코시분포의 형태는 다음과 같다.
따라서 log-likelihood는 다음과 같다.
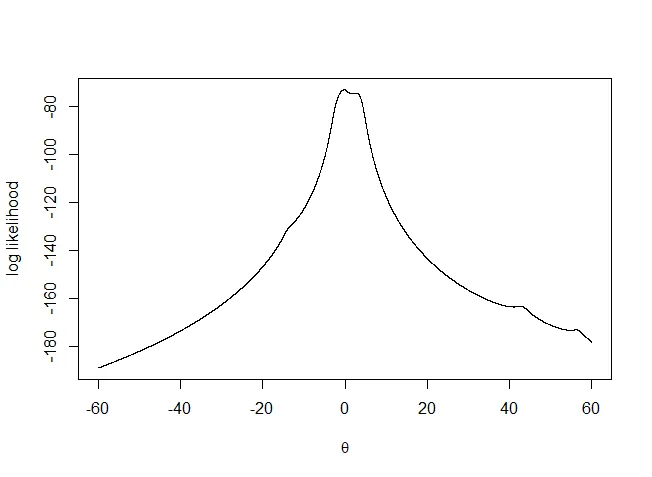
그럼 앞선 데이터를 활용하여 log-likelihood function을 plot으로 그려보면 다음과 같다.
→ 얼추 0에서 최대값을 갖는 것으로 보인다.
log-likelihood function을 미분하면,
따라서 의 해를 찾으면 코시분포의 MLE를 찾을 수 있다.
#setup
a = -1
b = 1
x = a+(b-a)/2
itr = 40
g.prime <- function(theta){
2*sum((mydata-theta)/(1+(mydata-theta)^2))
}
#bisection model
for (i in 1:itr){
if (g.prime(a)*g.prime(x) < 0) {b = x}
else {a = x}
x = a+(b-a)/2
}
x
R
복사
-0.1922866
R의 내장함수를 이용하여 MLE를 찾아보면 -0.1922866과 근사한 값이 나오는 것을 확인할 수 있다.
optimize(function(theta) -sum(dcauchy(mydata, location=theta, log=TRUE)), c(-50,50))
R
복사
$minimum
[1] -0.1922667