출처:
1. 정규화의 정의
정규화란 모델 복잡도에 대한 일종의 패널티로, Overfitting 을 예방하고 Generalization(일반화) 성능을 높이는데 도움을 준다. 딥러닝과 머신러닝의 Regularization 방법으로는 L1 Regularization, L2 Regularization, Dropout, Early stopping 등이 있다.
2. L1-Norm, L2-Norm
모델에서 학습을 진행할 때, 학습 데이터에 따라 특정 weight의 값이 커지게 될 수있다. 이렇게 되면 과적합이 일어날 가능성이 아주 높은데, 이를 방지하기 위해 L1, L2 regularization를 사용한다. 각각은 l1 -norm , l2 - norm의 컨셉을 가져와 학습에 영향을 미치는 cost function을 조정한다.
•
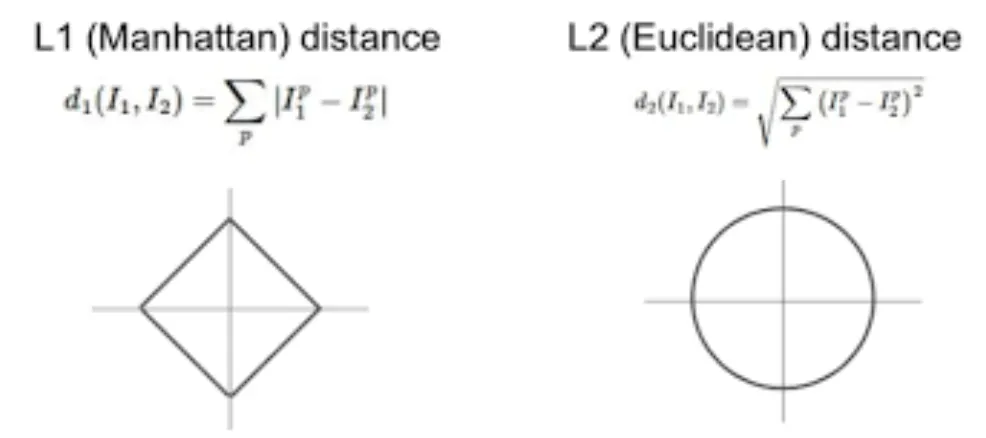
L1 Norm 은 벡터 p, q 의 각 원소들의 차이의 절대값의 합
•
L2 Norm 은 벡터 p, q 의 유클리디안 거리(직선 거리)
3. L1 Regularization
더하기 전 좌측이 일반적인 cost function이고 여기에 가중치 절대값을 더해준다.
편미분 을 하면 w값은 상수값이 되어버리고, 그 부호에 따라 +-가 결정된다. 가중치가 너무 작은 경우는 상수 값에 의해서 weight가 0이 된다.
⇒ 결과적으로 몇몇 중요한 가중치들만 남게 됨.
4. L2 Regularization
Cost function에 제곱한 가중치 값을 더해줌으로써 편미분 을 통해 back propagation 할 때 Cost 뿐만 아니라 가중치 또한 줄어드는 방식으로 학습을 한다. 특정 가중치가 비이상적으로 커지는 상황을 방지하고, Weight decay가 가능해진다.
⇒ 전체적으로 가중치를 작아지게 하여 과적합을 방지.
5. 선형 회귀 모델에의 적용
•
선형 회귀 모델에서 L1 규제를 주는 것이 lasso regression
•
선형 회귀 모델에서 L2 규제를 주는 것이 Ridge regression
•
elasticnet 은 두 개 다 쓰는 것 → L1 규제와 L2 규제를 모두 쓰되 비중을 다르게 함.
6. L1 Regularization VS L2 Regularization
L1을 적용하면 vector들이 sparse vector가 되는 경향이 있다. 즉, 작은 weight 값이 0이 된다. 따라서 weight 수를 줄이고 small set을 만들고 싶으면 L1을 사용할 수 있다. (feature selection) L2는 모든 가중치를 균등하고 작게 유지하려고 하므로, 일반적으로 학습 시 더 좋은 결과를 만든다.
•
왜 L1은 sparse vector를 만들고 L2는 균등하게 작은 weight들을 만들까?
•
만약 (1,0) vector가 있을 때, L1으로 계산하면 |1|+|0|=1이 되고 L2로 계산하여도 1+0=1이 된다. 반면 (0.5,0.5) vector가 있을 때, L1으로 계산하면 |0.5|+|0.5|=1이 되지만 L2로 계산하면 0.52+0.52=0.25+0.25=0.5가 된다. 값이 균등하게 작을 때에는 L2의 값이 더 작아지게 된다. 따라서 Error에 더 작은 penalty를 주게 된다.
(1,0)
|1|+|0|=1
1+0=1
(0.5,0.5)
|0.5|+|0.5|=1
0.52+0.52=0.25+0.25=0.5
•
L1, L2 연산한 값을 Error에 더하므로 연산 결과가 작아지는 값을 선호한다. 이 값이 너무 커져 버리면 오히려 학습하는 데 방해가 될 수 있기 때문이다. 따라서 L1 보다 L2를 많이 사용하는 이유이기도 하다.