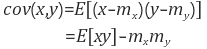목차
출처
1. PCA(Principal Component Analysis) 정의
PCA란 분포된 데이터들의 주성분(Principal Component)를 찾아주는 방법이다.
PCA는 데이터 하나 하나에 대한 성분을 분석하는 것이 아니라 여러 데이터가 모여 하나의 분포를 이룰 때 이 분포의 주성분을 분석해주는 방법이다.
그리고 주성분은 그 방향으로 데이터들의 분산이 가장 큰 방향벡터를 의미한다.
데이터들의 분산이 크다는 것은 데이터에 대한 정보가 그만큼 많다는 것을 의미한다.
어떠한 한 학급을 예로 들어보자. 어떤 학급을 분석할 때 나이와 키 중에 어떤 것이 더 의미가 있을까? 물론 학교를 조금 일찍 들어가거나 늦게 들어가는 것 등의 이유로 인해 학생들의 나이가 조금씩 차이는 있을 수 있지만 대부분 같은 나이일 것이다. 그렇지만 키는 굉장히 다양하게 분포되어 있을 가능성이 높다. 즉, 분산이 큰 것이다. 이러한 점에서 데이터는 분산이 작은 것보다 클 때 정보량이 더 많은 것을 알 수 있다.
2. PCA의 계산
PCA를 알기 위해서는 먼저 공분산 행렬(Covariance Matrix)에 대해서 알아야 한다.
우선 x와 y의 공분산(Covariance)은 다음과 같이 정의된다.
이 때 는 각각 x와 y의 평균.
그리고 공분산 행렬이란 데이터의 좌표 성분들 사이의 공분산 값을 원소로 하는 행렬로서 데이터의 i번째 좌표 성분과 j 번째 좌표 성분의 공분산 값을 행렬의 i행 j열 원소값으로 하는 행렬이다.
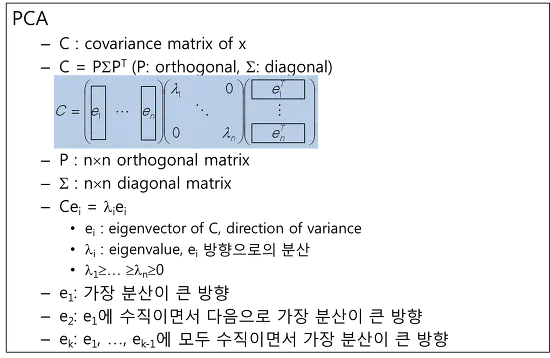
그리고 PCA는 입력 데이터들의 공분산 행렬에 대한 고유값분해라고 볼 수 있다. 이 때 나오는 고유벡터가 주성분 벡터로서 데이터의 분포에서 분산이 큰 방향을 나타내고, 대응되는 고유값이 그 분산의 크기를 나타낸다.
3. PC 선정방법
보편적인 규칙은 없고, 경험에 의한 법칙만 있다.
1.
설명된 분산의 축척 비율이 적어도 80% 이상이어야 한다.
2.
scree plot에서 elbow 지점이 존재하면 그 지점 이전까지의 PC들을 선택한다.
3.
개별 고유값이 1이상인 주성분을 고르는 것이 좋다.