////
Search

Bootstrapping

단원
Resampling
목차

1. 정의

부트스트랩핑(Bootstrapping)은 데이터셋을 리샘플링하여 다수의 시뮬레이션 샘플을 생성하는 통계 방법이다. 해당 방법을 사용하는 이유는 우리가 관심 있는 통계량의 표준오차와 신뢰 구간 등을 구하고 가설검정을 수행하기 위함이다. 기존의 가설 검정은 모수적 방법으로, 특정 분포를 가정하지만 부트스트랩핑 방법은 비모수적 방법으로 분포 가정이 필요없다는 장점이 있다.

2. 리샘플링(Resampling)

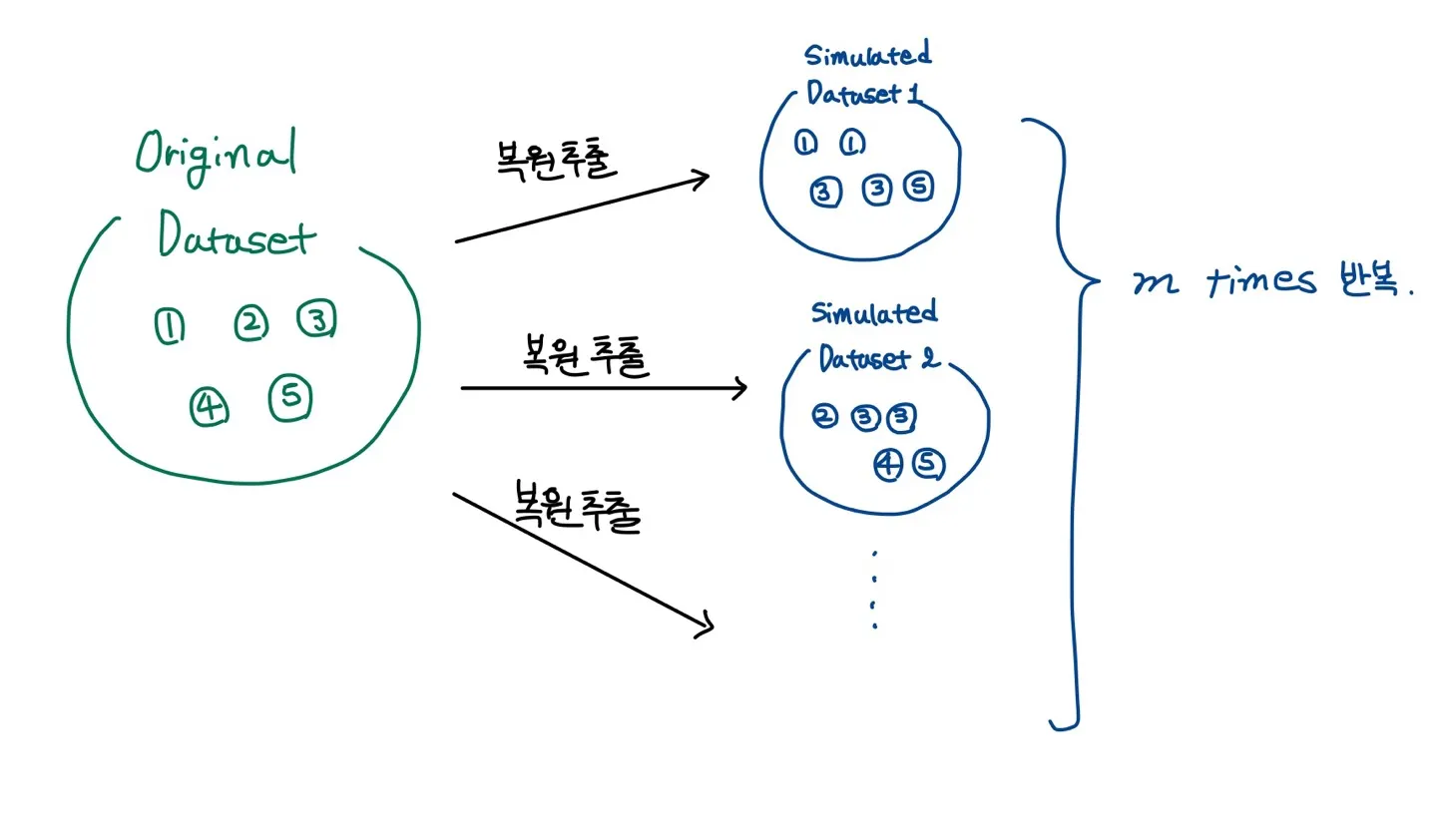
부트스트래핑은 기존의 원래 데이터셋을 복원 추출하여 시뮬레이션 데이터셋을 생성하며 리샘플링이 작동하는 방식은 다음과 같다.
•
리샘플링시에 각 데이터를 추출할 확률은 전부 동일하다.
•
각 데이터들은 중복하여 추출될 수 있다(복원 추출). 즉, 뽑힌 데이터가 또 뽑힐 수 있다.
•
리샘플링된 데이터셋은 기존 데이터셋의 크기와 동일해야 하며 리샘플링된 데이터셋을 여러 번(수백~수천번) 구한다.

3. 활용 예시

표본 평균의 신뢰 구간

가장 간단한 예시는 표본 평균의 신뢰 구간을 구하는 것이다. 예를 들어 어떤 학급의 학생들을 대상으로 키를 조사했다고 하자.
각 학생들의 키는 x1,x2,....xnx_1, x_2, .... x_n 이며 평균이 Xˉ\bar{X}라고 하자. 이때 부트스트래핑 방식으로 Xˉ\bar{X}의 95%신뢰구간을 구해보자.
우선 기존의 데이터셋인 {x1,x2,....xn}\{ x_1,x_2, .... x_n \}에서 n개의 데이터를 중복을 허용하여 뽑는 것을 m번 반복하자.
{x1,x1,x9,......,x50}{x4,x5,x5,......,x54}{x3,x4,x5,......,x47}⋮\{x_1,x_1,x_9,......,x_{50} \} \\ \{x_4,x_5,x_5,......,x_{54} \} \\ \{x_3,x_4,x_5,......,x_{47} \} \\ \vdots
그리고 각각의 시뮬레이션 데이터셋에서 표본 평균을 구한다. Xˉ1,Xˉ2,...,Xˉm\bar{X}_1, \bar{X}_2, ..., \bar{X}_m
그 다음 m 개의 표본 평균을 순서대로 나열하여 97.5th percentile 값과 2.5th percentile 값을 구한다. 예를 들어 97.5th percentile 값을 178.4, 2.5th percentile 값을 169.5라고 하자.
그러면, 부트스트래핑 방법으로 구한 표본 평균의 신뢰구간은 [169.5,178.4][169.5, 178.4]이다.

Bootstrapping Regression

회귀분석에서 계수에 대한 분포도 Bootstrapping 방식으로 구해볼 수 있다.
n개의 데이터로 구성되어 있는 데이터 셋 {(x1,y1),...,(xn,yn)}\{ (x_1, y_1), ..., (x_n, y_n) \} 을 가정하자. 그리고 회귀분석을 통해서 얻어낸 회귀계수의 추정치를 β^\hat{\beta} 라고 하자. 이때 β^\hat{\beta}의 분포를 부트스트래핑 방식으로 구해보자.
우선 주의해야 할 점은 yi∣xiy_i | x_i 가 iid가 아니라는 점이다. 즉, X와 Y는 독립관계가 아니다. (not independent) 따라서 복원 추출을 시행할 때 (xi,yi)(x_i, y_i)를 기준으로 추출해서는 안 된다.
대신 우리는 잔차(residual)들이 독립이라는 점을 이용한다. 회귀 분석을 진행할 때 우리는 잔차가 독립성 가정을 만족한다고 가정한다.
ϵ^i∼iidN\hat{\epsilon}_i \overset{\underset{\mathrm{iid}}{}}{\sim} N
이때 fitted value가 yi^\hat{y_i}라고 했을 때 yi=y^i+ϵ^iy_i = \hat{y}_i + \hat{\epsilon}_i 이다.
따라서 우리는 (xi,yi)(x_i, y_i) 대신에 {ϵ^1,...ϵ^n}\{ \hat{\epsilon}_1, ... \hat{\epsilon}_n \}을 부트스트래핑한다. 그리고 그 시뮬레이션 잔차들을 이용하여 pseudo-responses들을 만들고 이를 이용하여 시뮬레이션 계수들을 구한다. 이를 정리하면 다음과 같다.
1.
기존의 데이터셋 {(x1,y1),...,(xn,yn)}\{ (x_1, y_1), ... , (x_n, y_n) \}를 이용하여 회귀계수(β^)(\hat{\beta})를 구한다.
2.
회귀계수를 통해 fitted value(y^i)(\hat{y}_i)와 fitted residual(ϵ^i)(\hat{\epsilon}_i)를 도출한다.
3.
잔차의 집합({ϵ^1,...,ϵ^n})(\{\hat{\epsilon}_1, ... , \hat{\epsilon}_n \} )을 복원 추출하여 시뮬레이션 데이터 데이터셋({ϵ^1∗,...,ϵ^n∗})(\{\hat{\epsilon}_1^*, ..., \hat{\epsilon}_n^*\})을 생성한다.
4.
i=1,...ni = 1,... n에 대하여 bootstrap set of pseudo-responses를 생성한다. Yi∗=y^i+ϵi∗^Y_i^* = \hat{y}_i + \hat{\epsilon_i^*}
5.
Y∗Y^*를 x\mathbf{x}에 대하여 회귀분석하여 bootstrap parameter estimate인 β^∗\hat{\beta}^*를 구한다.
6.
3-5를 m번 반복한다.