목차
문제
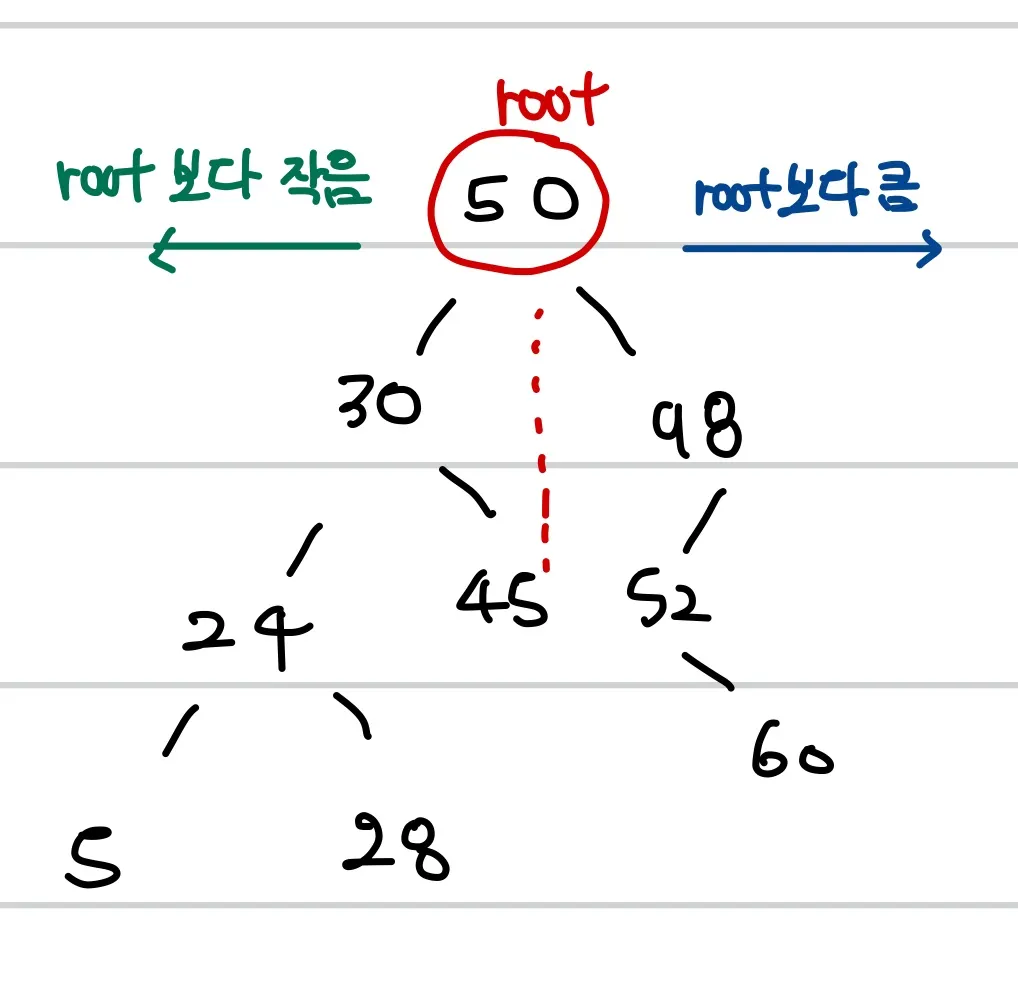
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
•
노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
•
노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
•
왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.
이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
입력
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.
출력
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.
예제
입력
50
30
24
5
28
45
98
52
60
Plain Text
복사
출력
5
28
24
45
30
60
52
98
50
Plain Text
복사
풀이
import sys
sys.setrecursionlimit(10**9)
pre_list = [] # 전위 순회 list
while True:
try:
pre_list.append(int(input()))
except:
break
# 후위 순회 출력 함수
def post_order(start, end, pre_list):
if start > end: # 탐색 범위가 옳지 않은 경우 함수 중단
return
root = pre_list[start] # 루트 값
point = start+1 # 분기점 탐색 시작점
# 분기점 탐색
while point <= end: # end를 넘어갈 수는 없다.
if pre_list[point] > root: # 분기점을 찾은 경우
break # break
point += 1 # 오른쪽으로 하나씩 탐색해봄.
post_order(start+1, point-1, pre_list) # 왼쪽 서브 트리 탐색
post_order(point, end, pre_list) # 오른쪽 서브 트리 탐색
print(root) # 루트 출력
post_order(0, len(pre_list)-1, pre_list)
Python
복사
처음에는 트리를 쌓은 다음 후위 순회를 출력하는 함수를 사용해서 문제를 풀려고 했으나 시간 초과가 발생했다. 그래서 다른 사람들의 답을 열심히 참고했다.....
문제 풀이의 포인트는 전위 순회는 우선 root를 출력하고 왼쪽 서브 트리와 오른쪽 서브 트리를 순서대로 출력한다는 점을 이용하는 것이다. 따라서 우리가 해야 되는 것은 root / 왼쪽 서브 트리 / 오른쪽 서브 트리 를 찾는 것이다. root는 처음에 나오니까 바로 찾을 수 있고 왼쪽 서브 트리와 오른쪽 서브 트리를 구별하는 것은 root보다 커지는 값이다. 트리의 구조를 생각하면 당연하다.
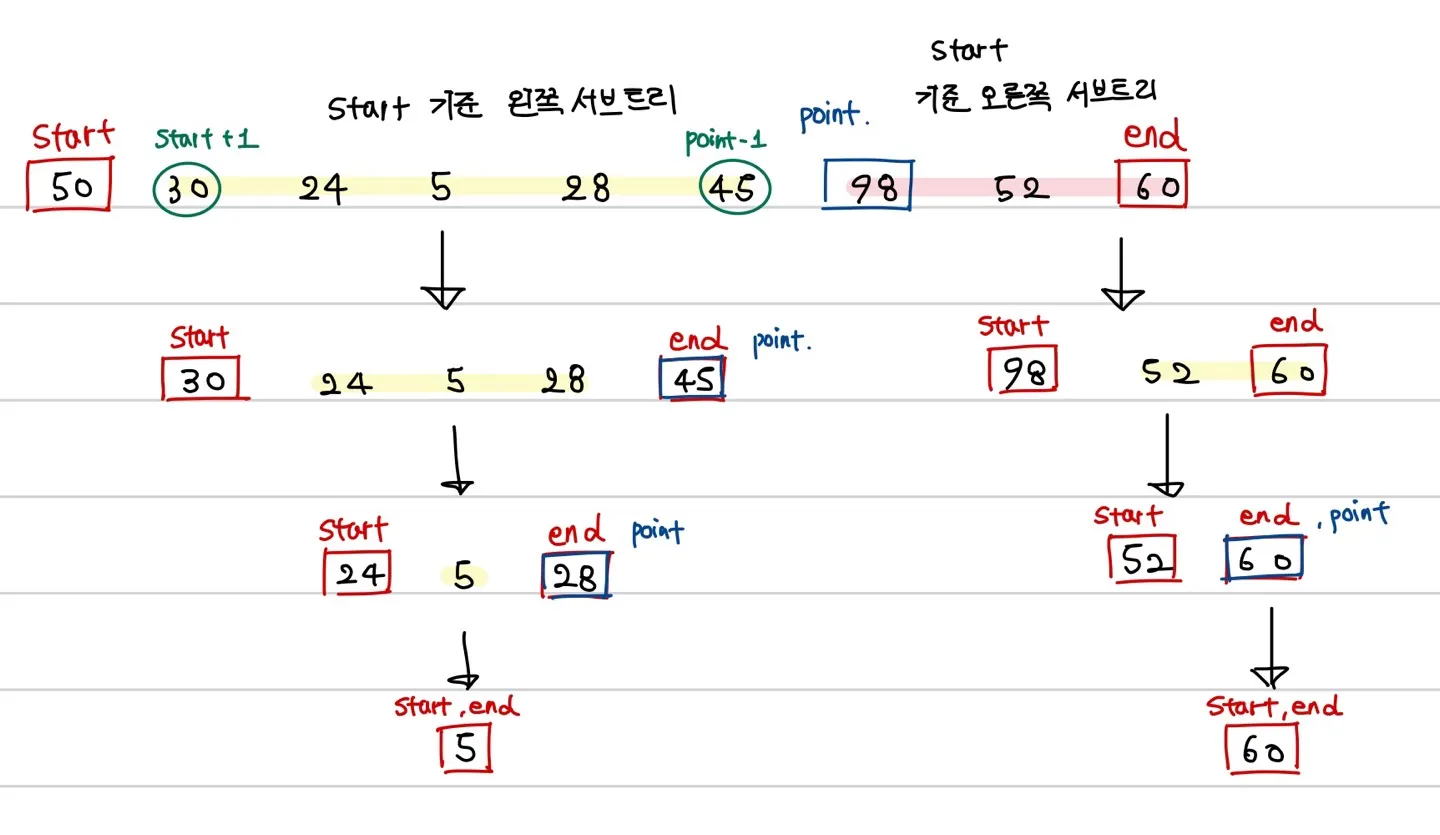
예제를 예시로 들면 50을 맨 처음 root로 잡았을 때 98이 root인 50보다 커지는 값이기 때문에 98을 구분점으로 해서 30~45까지는 왼쪽 서브 트리, 98부터 60까지는 오른쪽 서브 트리로 잡는다.
따라서 우리는 우선 1) 탐색 범위를 설정하고 2) 구분점을 발견한 다음 3) 왼쪽 서브 트리를 출력하고 4) 오른쪽 서브 트리를 출력한 다음 5) 마지막으로 root를 출력해야 한다.
결국 탐색 범위를 인자로 갖는 함수를 구축해야 한다.
post_order(탐색 시작 point, 탐색 끝 point, 전위 순회 리스트)
그 다음 구분점을 발견해야 한다. 구분점은 root의 오른쪽 point 부터 시작해서 탐색 끝 point까지 존재가능하다.
그런데 탐색을 진행하면 구분점이 없는 경우가 발생한다. 왼쪽 서브 트리만 존재하거나 오른쪽 서브 트리만 존재하는 경우 또는 둘 다 존재하지 않는 경우이다. 이러한 경우 탐색 시작 point가 탐색 끝 point보다 커지는 경우 아무것도 출력하지 않도록 만들면 해결된다.
구분점을 발견한 경우 구분점을 기준으로 왼쪽 서브 트리와 오른쪽 서브 트리를 각각 출력해야 한다.
위의 과정이 다 끝나면 마지막으로 root를 출력한다.
이를 그림으로 표현하면 다음과 같다.
기억할 점
•
입력 횟수가 주어지지 않는다면 while문과 try except 문을 활용할 수 있다.
•
함수를 만들때 아무것도 출력하고 싶지 않다면 return을 쓴 뒤 공백으로 두면 된다.