////
Search

Newton-Cotes Quadrature

단원
Numerical Integration
목차

1. 뉴턴-코츠 구적법(Newton-Cotes Quadrature)

어떤 구간의 적분을 구하려고 할 때 적분 함수를 구하지 못할 때가 있다. 그 때 우리는 수치적분(Numerical Integration) 방법을 사용할 수 있다. 수치적분이란 적분구간에 피적분함수를 포함한 적당한 급수의 합으로 근사하여 적분값을 수치적으로 구하는 것을 뜻한다. (출처: 위키백과)
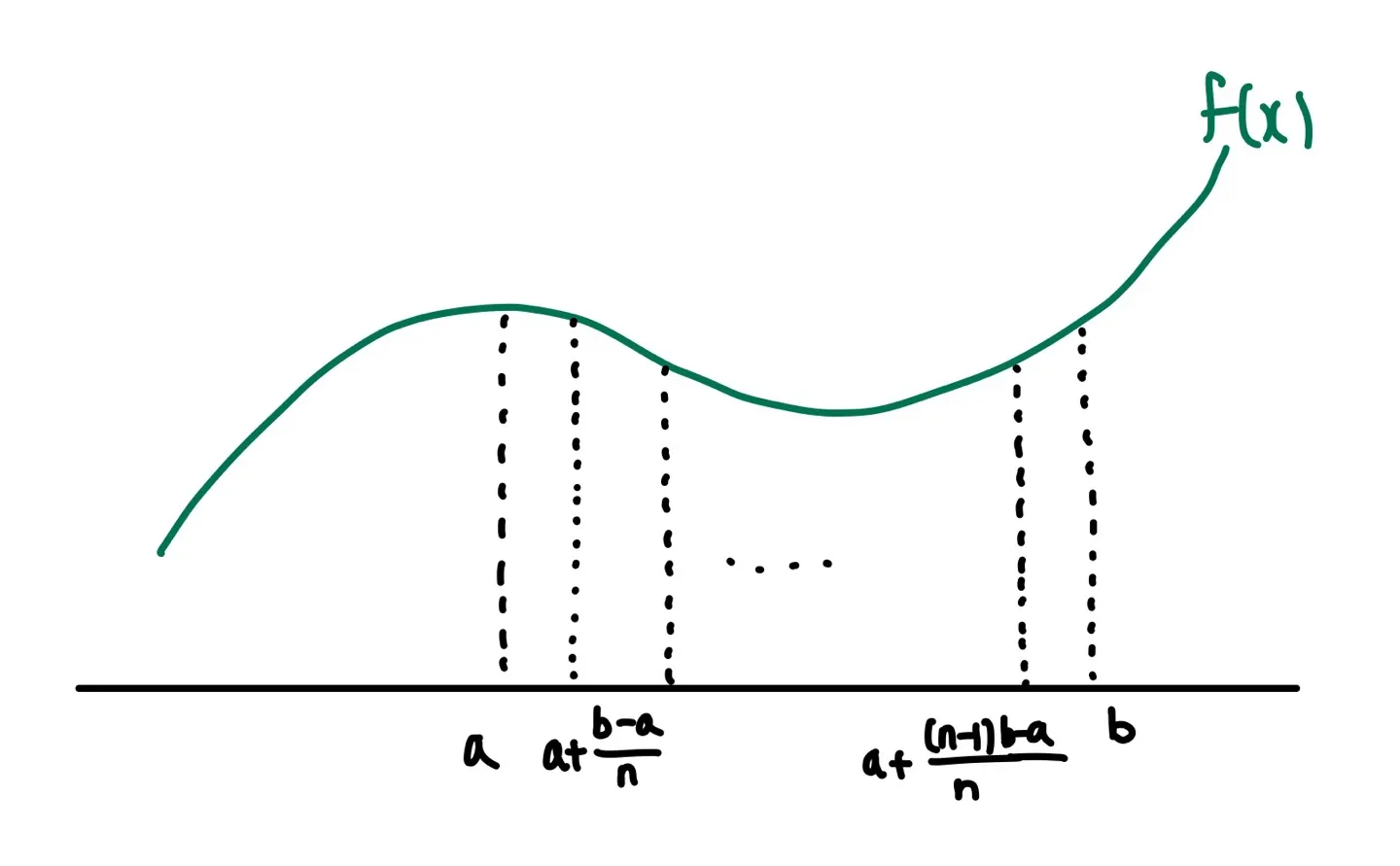
쉽게 얘기해서 적분 구간을 잘게 쪼개고 이를 이용하여 적분값을 근사적으로 구하는 것이다. 밑의 그림은 수치적분 중 뉴턴-코츠 구적법의 예시이다.
뉴턴-코츠 구적법(Newton-Cotes Quadrature)는 적분 구간을 전부 동일한 구간으로 쪼개어 적분값을 구하는 방식이다. 뉴턴-코츠 방식은 실제 적분값을 각 하위 구간에 대한 다항식 근사치로 대체한다. 무슨 말인지는 밑에서 좀 더 자세하게 살펴보자.
뉴턴-코츠 구적법은 쪼개는 방식에 따라서 다섯 가지 종류가 있다.
1.
리만 공식(Riemann rule)
2.
사다리꼴 공식(Trapezoidal rule)
3.
심슨 공식(Simpson’s rule)
4.
심슨의 3/8 공식(Simpson’s 3/8 rule)
5.
불 공식(Boole’s rule)

2. 리만 공식(Riemann Rule)

리만 공식(Riemann’s Rule)은 가장 간단한 방법으로 다음과 같dmfh이 근사한다.
∫abf(x)dx≈∑i=0n−1(xi+1−xi)f(xi),wherex0=a,xn=b\int^b_a f(\mathrm{x})d\mathrm{x} \approx \sum^{n-1}_{i=0}(x_{i+1}-x_{i})f(x_i), \\ \text{where} \quad x_0 = a, x_n = b
h=b−anh = \frac{b-a}{n} 라고 하면,
∫abf(x)dx≈∑i=0n−1hf(a+ih)≡R^(n)\int^b_a f(\mathrm{x})d\mathrm{x} \approx \sum^{n-1}_{i=0}hf(a+ih) \equiv \hat{R}(n)
으로 표현할 수도 있다. n의 크기를 키울수록 실제 적분값에 가까워진다.
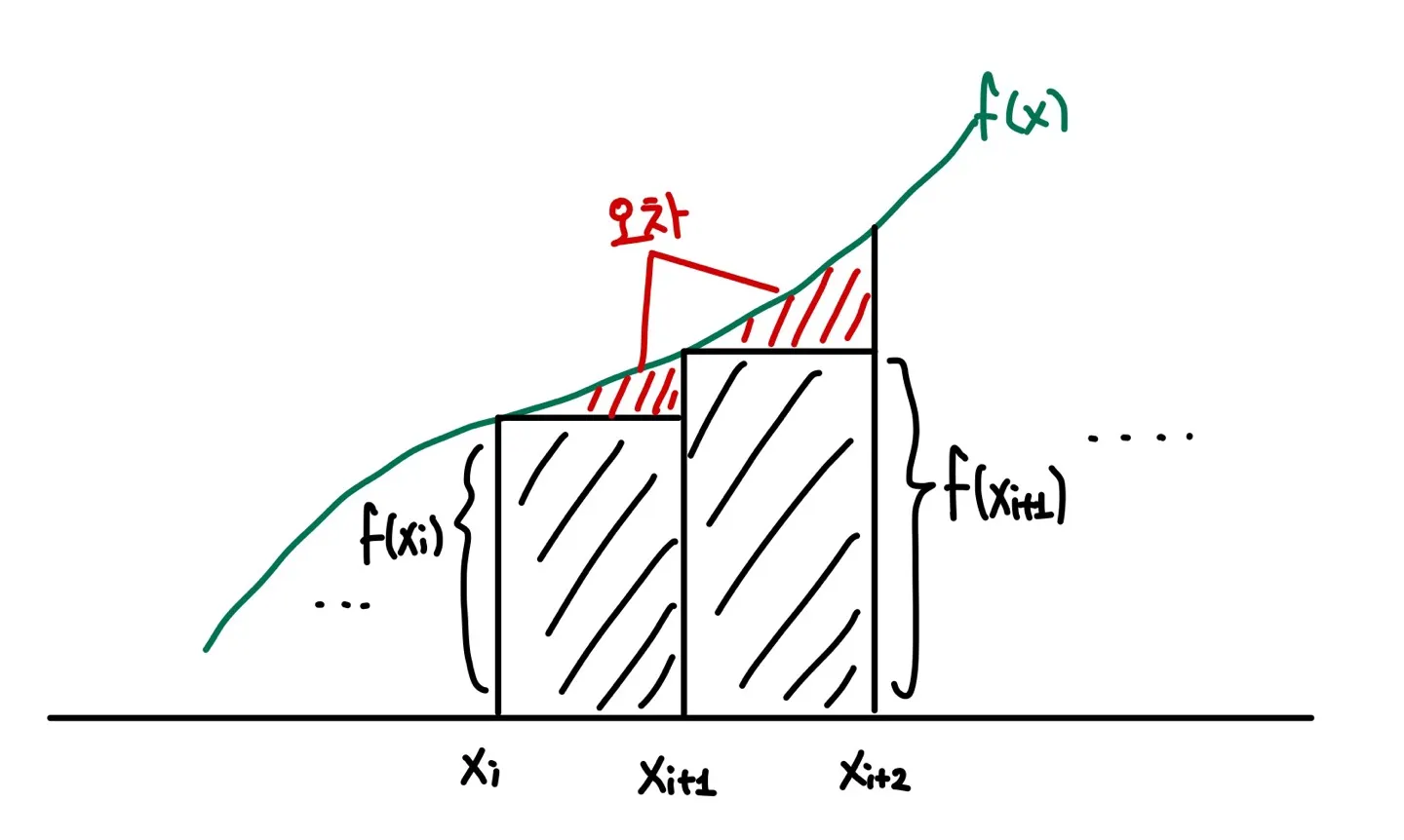
공식을 해석하면, 적분 구간을 무수히 작은 직사각형으로 채워넣어서 적분값을 구하는 방식인데, 그림을 통해 알아보자.
제일 간단한 방식이며 다만 오차가 크다는 단점을 가지고 있다.

3. 사다리꼴 공식(Trapezoidal Rule)

사다리꼴 공식(Trapezoidal rule)은 다음과 같이 정의된다.
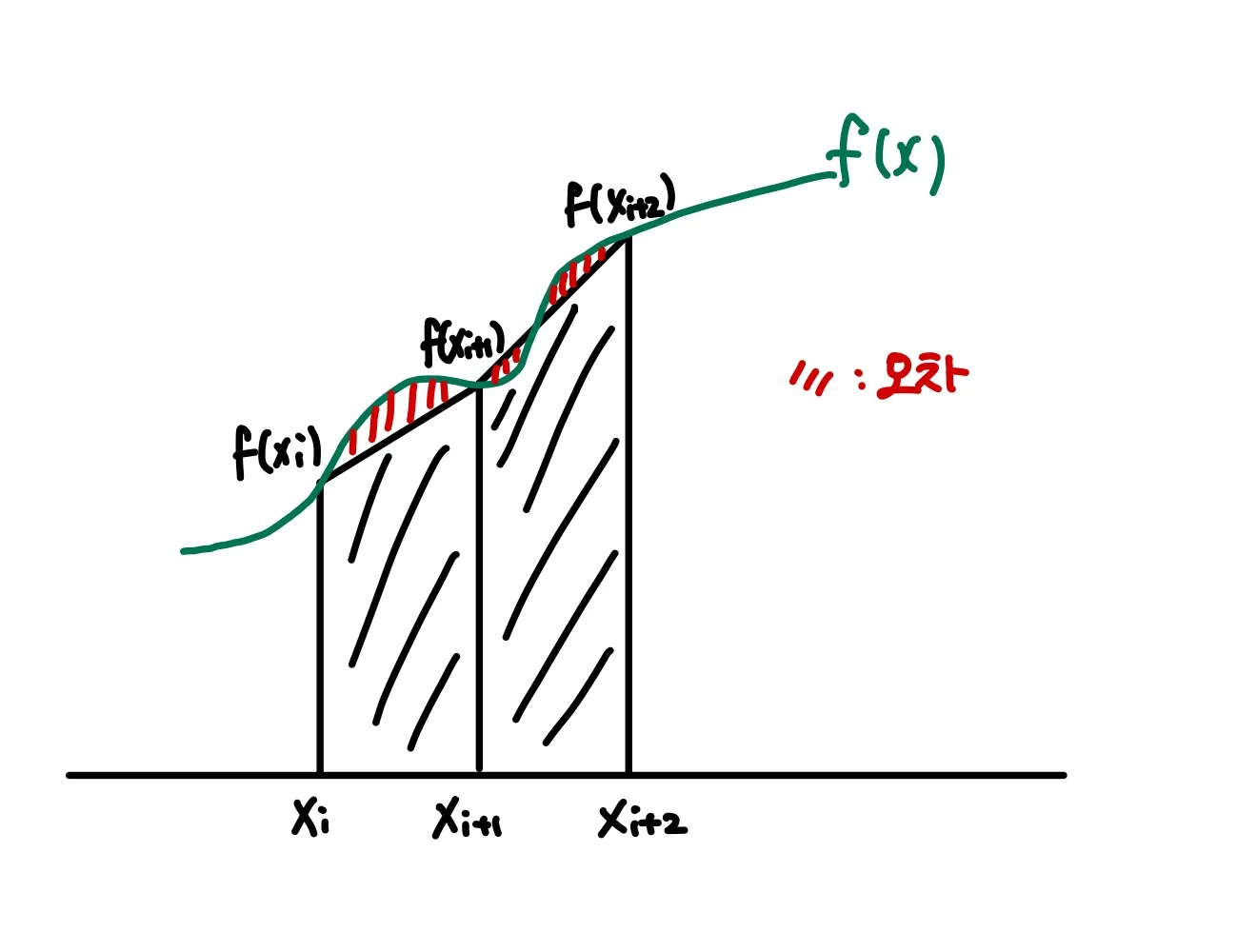
∫abf(x)dx≈∑i=0n−112(xi+1−xi)(f(xi)+f(xi+1))=h2f(a)+h∑i=1n−1f(a+ih)+h2f(b)≡T^(n)wherex0=a,xn=b,h=b−an\int^b_a f(\mathrm{x})d\mathrm{x} \approx \sum^{n-1}_{i=0}\frac{1}{2}(x_{i+1}-x_{i})(f(x_i)+f(x_{i+1})) \\ = \frac{h}{2}f(a) + h\sum^{n-1}_{i=1}f(a+ih) + \frac{h}{2}f(b) \equiv \hat{T}(n) \\ \text{where} \quad x_0 = a, x_n = b, h = \frac{b-a}{n}
그림으로 살펴보면,
이번에는 직사각형이 아니라 사다리꼴을 채워넣어서 구하는 방식이다. Riemann rule보다 조금 식이 복잡해지지만 오차가 줄어드는 장점이 있다.

4. 심슨 공식(Simpson’s Rule)

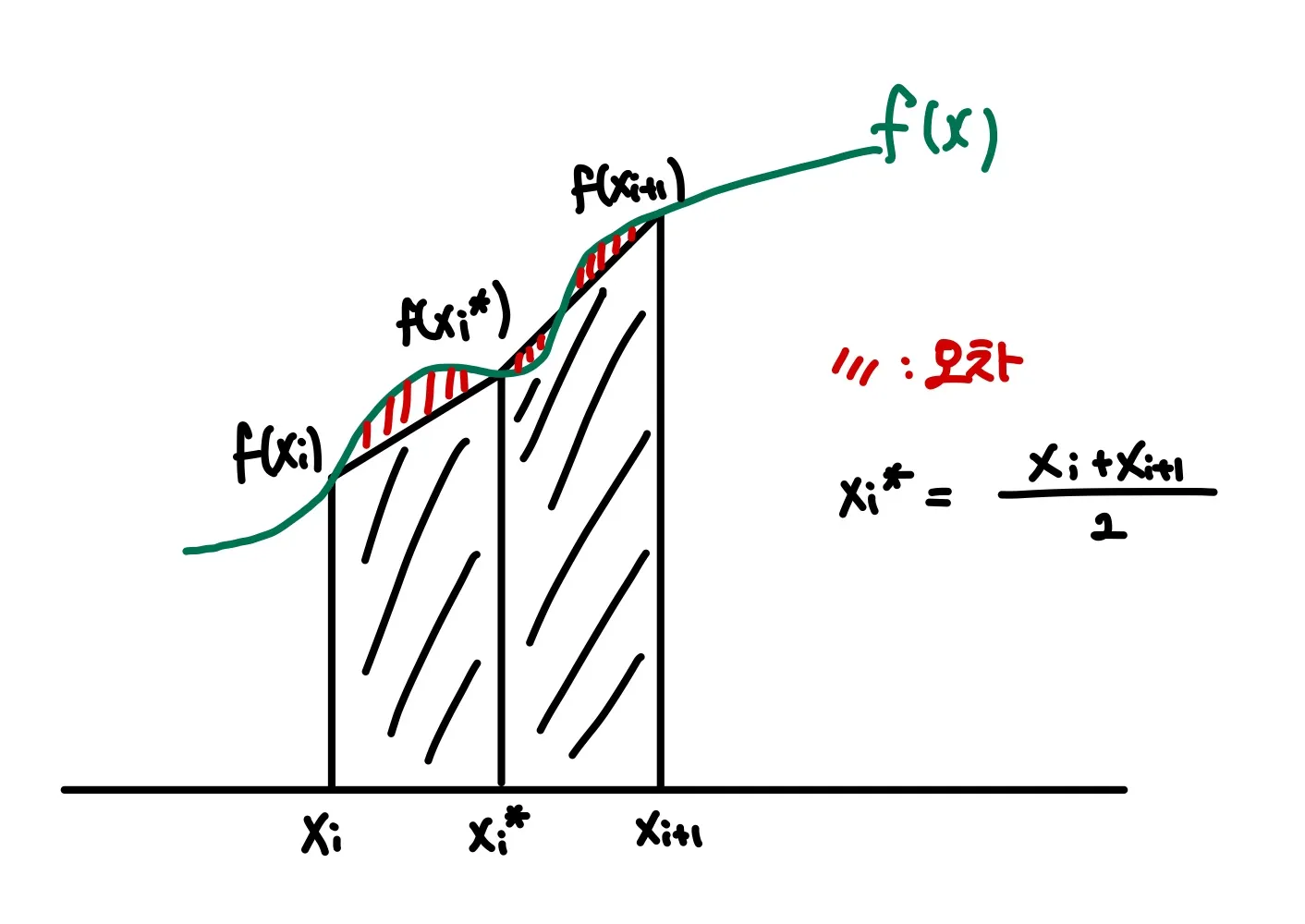
심슨 공식(Simpson’s Rule)은 xix_i와 xi+1x_{i+1} 사이에 중점을 잡고 사다리꼴을 두 개 만들어서 적분값을 근사하는 방식이다.
∫abf(x)dx≈h3∑i=1n/2(f(x2i−2)+4f(x2i−1)+f(x2i))≡S^(2n),whereh=b−an,n is even\int^b_af(\mathrm{x})d\mathrm{x} \approx \frac{h}{3}\sum^{n/2}_{i=1}(f(x_{2i-2}) + 4f(x_{2i-1})+f(x_{2i})) \equiv \hat{S}(\frac{2}{n}), \\ \text{where} \quad h = \frac{b-a}{n},\quad \text{n is even}
심슨 공식은 위의 두 방식보다 복잡하지만 오차가 더 작다는 장점이 있다.

5. 활용 및 code

Proportionality constant

수치적분은 굉장히 다양한 분야에서 사용될 수 있다. 그 중에서 Posterior 분포의 비례상수(또는 정규화 상수)를 구하는 문제를 풀어보자.
Posterior 분포의 정규화 상수는 ∫k×(prior)×(likelihood)  dθ=1\int k \times (prior) \times (likelihood) \; d\theta = 1 을 만족하는 kk 를 의미한다.
data가 (x1,...,x7)=(6.52,8.32,0.31,2.82,9.96,0.14,9.64)(x_1, ..., x_7) = (6.52, 8.32, 0.31, 2.82, 9.96, 0.14, 9.64)로 주어졌을 때, Likelihood는 N(μ,9/7)N(\mu, 9/7) 이고 μ\mu에 대한 prior는 Cauchy(5,2)\text{Cauchy}(5,2)라고 하자. 이 때 posterior 분포의 정규화 상수(normalizing constant)를 뉴튼-코튼 구적법들을 통해 구해보자.
R과 Rcpp를 사용하여 code를 작성하였다.
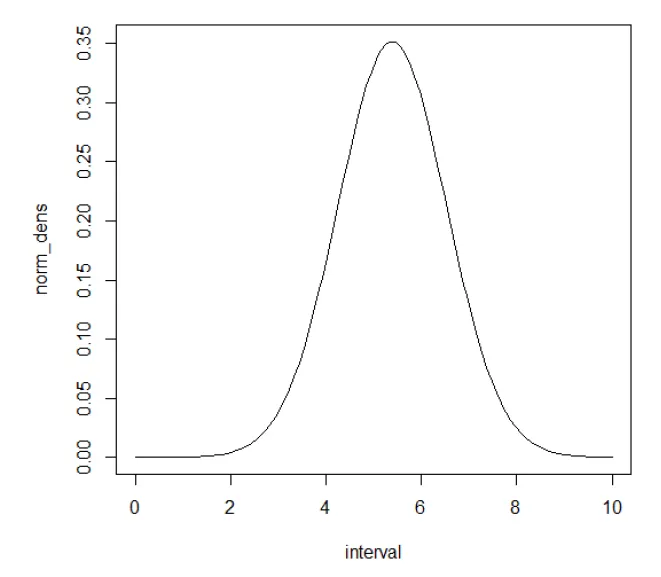
우선 적분의 구간을 구하기 위하여 plot을 한번 그려보자.
#data x = c(6.52, 8.32, 0.31, 2.82, 9.96, 0.14, 9.64) x_mean <- mean(x) sd <- sqrt(9/7) #범위를 대략적으로 지정해주기 위해서 plot을 한 번 그려보자. interval <- seq(0,10, length.out = 100) norm_dens <- dnorm(interval, mean=x_mean, sd=sd) plot(interval, norm_dens, type='l')
R
복사
→ 대략 0에서 10으로 적분 구간을 잡아보자.
interval <- c(0,10)
R
복사
cpp 함수 구현
우선 Rcpp에 cauchy pdf를 구해주는 함수는 없는 듯 하여 먼저 그것을 만들어주었다.
double cauchy_pdf(double x, double a, double b){ double y = (x - a) / b; double res = 1.0 / (datum::pi * b * (1.0 + y * y)); return(res); } vec cauchy_pdf_vec(vec x, double a, double b){ vec res; vec y; vec a_vec(x.n_rows); vec b_vec(x.n_rows); vec pi_vec(x.n_rows); vec ones(x.n_rows, fill::ones); a_vec.fill(a); b_vec.fill(b); pi_vec.fill(datum::pi); y = ( x - a_vec ) / b_vec; res = ones / ( pi_vec % b_vec % ( ones + y % y ) ); return res; }
C++
복사
다음으로는 Likelihood * Prior 함수를 만들어주었다.
double f(double x, double mean, double sd){ double res = normpdf(x, mean, sd) * cauchy_pdf(x, 5.0, 2.0); return res; } vec f_vec(vec x, double mean, double sd){ vec res = normpdf(x, mean, sd) % cauchy_pdf_vec(x, 5.0, 2.0); return res; }
C++
복사
그 다음 주어진 함수에 대해 Riemann, Trapezoidal, Simpsons quadrature를 시행해주는 function을 만들었다.
// [[Rcpp::export]] double riemann_cpp(NumericVector interval, double n, double mean, double sd){ vec x(n); double h = (interval[1]-interval[0])/n; for(int i = 0; i<n; i++){ x[i] = interval[0] + i*h; } double res = h*accu(f_vec(x, mean, sd)); return(res); } // [[Rcpp::export]] double trapezoidal_cpp(NumericVector interval, double n, double mean, double sd){ vec x(n-1); double a = interval[0]; double b = interval[1]; double h = (b-a)/n; for(int i = 1; i < n; i++){ x[i-1] = a + i*h; } double low = h/2*f(a, mean, sd); double high = h/2*f(b, mean, sd); double middle = h*accu(f_vec(x, mean, sd)); double res = low + high + middle; return(res); } // [[Rcpp::export]] double simpsons_cpp(NumericVector interval, double n, double mean, double sd){ vec x(n+1); vec out(n/2); double a = interval[0]; double b = interval[1]; double h = (b-a)/n; for(int i = 0; i < n+1; i++){ x[i] = a + i*h; } for(int j = 0; j < n/2; j++){ out[j] = h/3*f(x[2*j], mean, sd); out[j] = out[j] + 4*h/3*f(x[2*j+1], mean, sd); out[j] = out[j] + h/3*f(x[2*j+2], mean, sd); } double res = accu(out); return(res); }
C++
복사
이제 미리 설정한 interval을 이용하여 적분을 시행한 뒤 역수를 취해주면 proportionality constant kk를 구할 수 있다.
∵k=1∫(prior)×(likelihood)dμ\because \quad k = \frac{1}{\int (prior) \times (likelihood)d\mu}
1/riemann_cpp(interval, 100, mean(x), sd) 1/trapezoidal_cpp(interval, 100, mean(x), sd) 1/simpsons_cpp(interval, 100, mean(x), sd)
R
복사
7.846575
7.846569
7.846569
따라서 kk는 약 7.8465