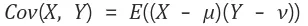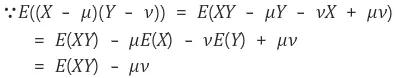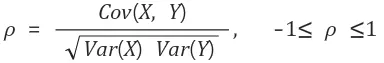1. 공분산(Covariance)
공분산(covariance)은 각 확률변수들이 어떻게 퍼져있는지를 나타내는 값이라고 해석할 수 있다.
두 확률변수 X와 Y를 가정하자. 이 때 두 확률변수 X와 Y에 대한 공분산은 다음과 같이 계산할 수 있다.
이 때, 는 각각 X와 Y의 평균이다.
즉, 공분산은 X의 편차와 Y의 편차를 곱한 것의 평균이다. 위의 식을 정리하면 아래와 같다.
이 때 X와 Y가 독립이라면 E(XY) = E(X)E(Y) 이므로 공분산은 0이 된다.
공분산 값에 따른 X와 Y의 관계는 다음과 같다.
1.
Cov(X,Y) > 0: X 값이 증가하면 Y 값도 증가한다.
2.
Cov(X,Y) < 0: X 값이 감소하면 Y 값이 증가한다.
3.
Cov(X,Y) = 0: X와 Y 간에 선형관계가 존재하지 않는다.
단, 이 때 주의할 것은 공분산의 값이 0이더라도 반드시 X와 Y가 독립은 아니라는 점이다. 독립인 경우 공분산이 0이 되는 것은 맞지만 역은 성립하지 않는다.
2. 상관계수(Correlation)
공분산의 문제점은 고정된 범위가 존재하지 않으며 X와 Y값의 단위에 영향을 받는다는 점이다. 따라서 우리는 단순히 공분산 값만을 보고 상관관계가 강한지 약한지 판단하기가 힘들다. 따라서 이를 보완하기 위해 나온 것이 상관계수(correlation)이다. 상관계수는 공분산을 각각의 확률변수의 분산들의 곱을 제곱근한 것으로 나누어준 것이다. 즉,
이 때, 상관계수의 중요한 특징은 반드시 -1에서 1사이의 값을 갖는다는 것이다. 따라서 확률변수의 크기에 상관없이 상관관계를 가늠할 수 있다는 장점이 있다.
1.
상관계수가 1에 가까울수록 두 확률변수는 양의 상관관계를 갖는다.
2.
상관계수가 -1에 가까울수록 두 확률변수는 음의 상관관계를 갖는다.
3.
상관계수가 0이면 두 확률변수 간에 선형관계가 존재하지 않는다.
주의해야 할 점은 상관계수 역시 어느 정도 이상이어야 상관관계가 있다라고 정해진 것이 없다는 것이다. 분야마다 판단되는 상관계수의 정도는 차이가 있다. 일반적으로는 0.6~0.7 정도의 절댓값을 가지면 양 또는 음의 상관관계가 있다고 파악한다.