목차
문제
이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.
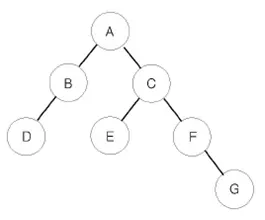
예를 들어 위와 같은 이진 트리가 입력되면,
•
전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
•
중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
•
후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
가 된다.
입력
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.
출력
첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.
예제
입력
7
A B C
B D .
C E F
E . .
F . G
D . .
G . .
Plain Text
복사
출력
ABDCEFG
DBAECFG
DBEGFCA
Plain Text
복사
풀이
import copy
import sys
sys.setrecursionlimit(10**9)
N=int(input())
tree_dict = {} # dictionary 형태로 tree 제작
for _ in range(N):
parent, left, right = input().split()
tree_dict[parent] = [left, right, False] # [왼쪽 자식 노드, 오른쪽 자식 노드, is_left]
# 'A'는 루트로 부모 노드 존재하지 않음
tree_dict['A'].append(None)
# 부모 노드 추가
for i in tree_dict:
left_c = tree_dict[i][0]
right_c = tree_dict[i][1]
if left_c != '.':
tree_dict[left_c][2] = True
tree_dict[left_c].append(i)
if right_c != '.':
tree_dict[right_c].append(i)
# 중위 순회시에 tree의 정보가 바뀌기 때문에 후위 순회용으로 copy
tree_dict2 = copy.deepcopy(tree_dict)
# 전위 순회
def preorder(start, tree, print_list):
print_list.append(start) # 루트 노드 프린트
if tree[start][0] != '.': # 만약 왼쪽 자식이 존재하면
preorder(tree[start][0], tree, print_list) # 내려감
if tree[start][1] != '.': # 왼쪽 자식들을 다 살펴본 후에 오른쪽 자식이 존재하면
preorder(tree[start][1], tree, print_list) # 내려감
# 중위 순회
def inorder(start, tree, print_list):
if tree[start][0] != '.': # 만약 왼쪽 자식이 존재하면
inorder(tree[start][0], tree, print_list) # 내려감
else: # 왼쪽 자식이 없는 경우
print_list.append(start) # 루트 노드 프린트
if tree[start][1] != '.': # 만약 오른쪽 자식이 존재하면
inorder(tree[start][1], tree, print_list) # 내려감
if tree[start][2]: # 오른쪽을 다 살펴본 후에 만약 현재 루트 노드가 왼쪽 자식에 해당하면
tree[tree[start][3]][0] = '.' # 루트 노드의 부모 노드의 왼쪽 자식 노드를 지우고
inorder(tree[start][3], tree, print_list) # 부모 노드로 올라감
def postorder(start, tree, print_list):
if tree[start][0] != '.': # 왼쪽 자식이 존재하면
postorder(tree[start][0], tree, print_list) # 내려감
elif tree[start][1] != '.': # 왼쪽 자식이 존재하지 않는데 오른쪽 자식이 존재하면
postorder(tree[start][1], tree, print_list) # 내려감
else: # 자식 노드가 존재하지 않으면
print_list.append(start) # 루트 노드 프린트
if tree[start][3] != None: # 만약 부모 노드가 존재하면
if tree[start][2]: # 루트 노드가 왼쪽 자식에 해당하는 경우
tree[tree[start][3]][0] = '.' # 루트 노드의 부모 노드의 왼쪽 자식을 지우고
postorder(tree[start][3], tree, print_list) # 부모 노드로 올라감
else:
tree[tree[start][3]][1] = '.' # 오른쪽 자식에 해당하면 오른쪽 자식을 지우고
postorder(tree[start][3], tree, print_list) # 부모 노드로 올라감
pre_print_list = []
inorder_print_list = []
postorder_print_list = []
preorder('A', tree_dict, pre_print_list)
inorder('A', tree_dict, inorder_print_list)
postorder('A', tree_dict2, postorder_print_list)
print(''.join(pre_print_list))
print(''.join(inorder_print_list))
print(''.join(postorder_print_list))
Python
복사
우선 Tree를 dictionary 형태로 제작했다.
Key 값은 Node를 의미하고 Value에는 [왼쪽 자식 노드, 오른쪽 자식 노드, 왼쪽 자식 여부, 부모 노드] 를 리스트의 형태로 넣었다.
왼쪽 자식 여부란 나의 부모 노드 관점에서 key node가 왼쪽 자식 노드인지 오른쪽 자식 노드인지를 가리킨다. (Bool 형태)
전위 순회와 중위 순회 후위 순회의 각각의 알고리즘은 다음과 같이 고안했다. 이때 내려가고 올라간다는 것은 자식이나 부모 노드로 이동해서 그 노드를 기준으로 다시 함수를 구현한다는 뜻이다.
1.
전위 순회
1) 자기 자신 print
2) 왼쪽 자식이 있으면 내려가기
3) 왼쪽을 다 살펴본 후 오른쪽 자식이 있으면 내려가기
2.
중위 순회
1) 왼쪽 자식이 있으면 내려가기
2) 왼쪽 자식이 없으면 자기 자신 print
2-1) 프린트 후에 오른쪽 자식이 있으면 내려감
2-2) 오른쪽을 다 살펴본 이후 만약 현재 node가 부모 노드의 왼쪽 자식이면 부모 노드의 왼쪽 자식을 지우고 부모 노드로 올라감
3.
후위 순회
1) 왼쪽 자식이 있으면 내려감
2) 왼쪽 자식이 없고 오른쪽 자식이 있으면 내려감
3) 둘 다 없으면 자기 자신 print
3-1) 만약 부모 노드가 존재하는 경우
3-2) 내가 왼쪽 자식이면 부모의 왼쪽 자식을 지우고 오른쪽 자식이면 부모의 오른쪽 자식을 지우고 부모 노드로 올라감
기억할 점
•
Node가 번호가 아니라 알파벳으로 설정되어 있는 경우 dictionary로 tree를 저장할 수 있다.
•
각각의 알고리즘을 외워두기