목차
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
예제
입력
3
1 2 3
1 3 2
Plain Text
복사
출력
2 1 3
Plain Text
복사
풀이
import sys
sys.setrecursionlimit(10**9)
N = int(input())
inord_list = list(map(int, sys.stdin.readline().split()))
postord_list = list(map(int, sys.stdin.readline().split()))
inord_index = {}
for i in range(N):
inord_index[inord_list[i]] = i # 나중에 root의 index를 찾을 때 .index()를 사용하면 시간이 너무 오래 걸림.
# 후위 순회 방법
def pre_maker(in_left, in_right, post_left, post_right):
if (post_left > post_right): # 탐색 범위가 맞지 않는 경우
return
root = postord_list[post_right] # 루트 노드
print_list.append(root) # 루트 노드의 값 출력
root_index = inord_index[root] # 전위 순회 리스트에서 루트 노드의 위치
pre_maker(in_left, root_index-1, post_left ,post_left+root_index-in_left-1) # 왼쪽 서브 트리 탐색
pre_maker(root_index+1, in_right, post_left+root_index-in_left, post_right-1) # 오른쪽 서브 트리 탐색
print_list = []
pre_maker(0, N-1, 0, N-1)
print(*print_list)
Python
복사
이번 문제도 다른 사람들의 답을 열심히 참고했다 ..
우선 솔루션 포인트는 각 오더 방식들의 순회 순서를 이용하는 것이다.
인 오더: 1) 왼쪽 서브 2) 루트 3) 오른쪽 서브
포스트 오더: 1) 왼쪽 서브 2) 오른쪽 서브 3) 루트
프리 오더: 1) 루트 2) 왼쪽 서브 3) 오른쪽 서브
이다. 따라서 인 오더와 포스트 오더의 리스트를 비교하여 왼쪽 서브와 오른쪽 서브 그리고 루트를 구별해야 한다.
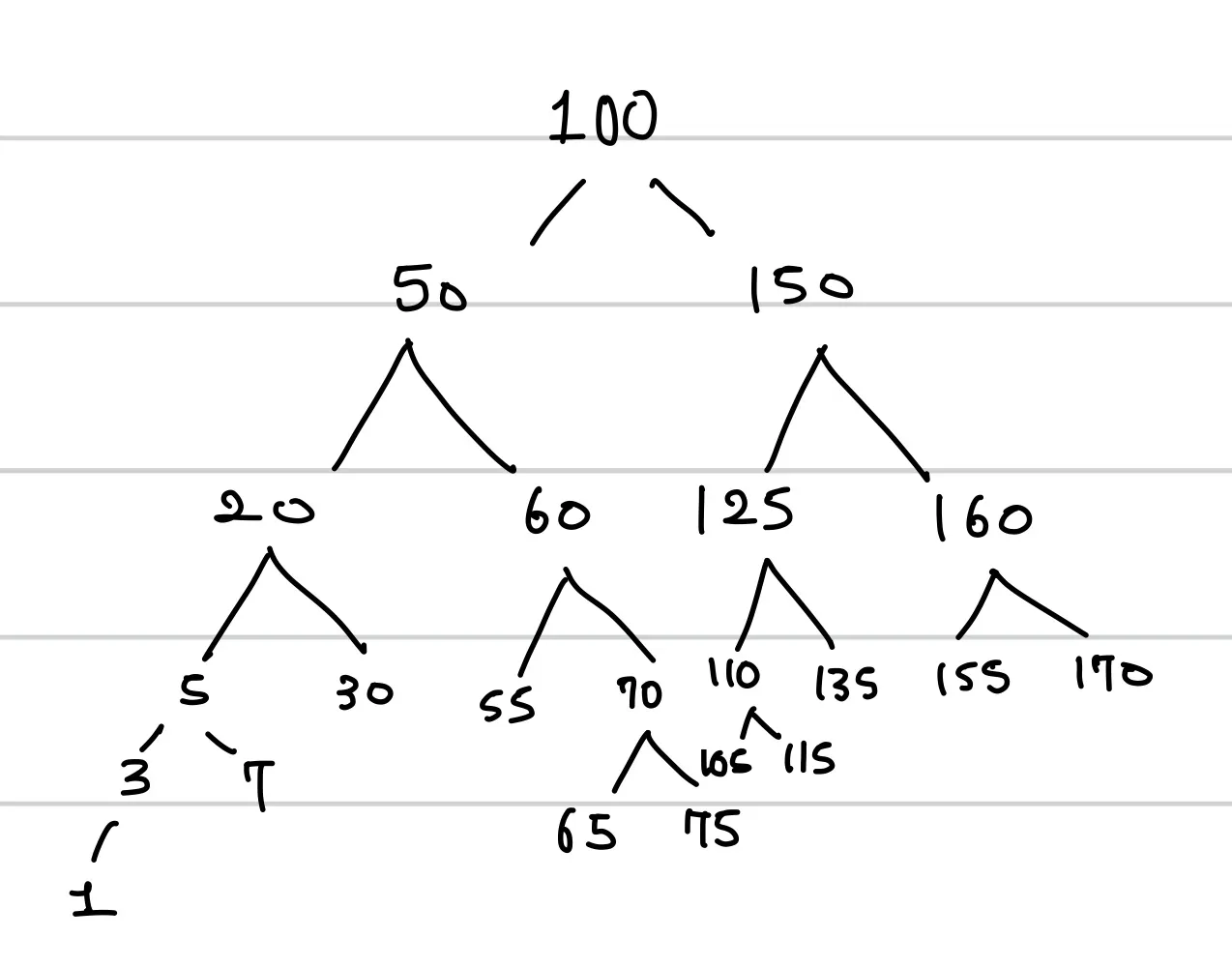
예제가 불친절하므로 새로운 트리를 하나 생성하자.
그럼 프리 오더와 인 오더 그리고 포스터 오더 방식에 따른 출력은 다음과 같을 것이다.
여기서 주목할 점은 탐색 범위의 마지막이 루트로 끝난다는 점이다. 따라서 우리는 맨 처음 출력되는 루트가 무엇인지 바로 알 수 있다. 그런데 포스트 오더만으로는 왼쪽 서브 트리와 오른쪽 서브 트리를 구별하지 못한다. 그런데 인 오더 방식은 1) 왼쪽 서브 트리 2) 루트 3) 오른쪽 서브 트리 순으로 순회를 진행하기 때문에 만약 인 오더에서 루트를 찾는다면 루트를 기준으로 왼쪽은 왼쪽 서브 트리 루트를 기준으로 오른쪽은 오른쪽 서브 트리가 될 것이다.
따라서
1.
포스트 오더 탐색 범위에서 루트를 찾고 (맨 마지막 값)
2.
인 오더 리스트에서 루트의 인덱스를 찾은 다음
3.
왼쪽은 왼쪽 서브 트리로 오른쪽은 오른쪽 서브 트리로 간주한다.
4.
그 다음 왼쪽 서브 트리에서 1-3 step을 반복한다.
5.
왼쪽 서브 트리가 끝나면 오른쪽 서브트리에서 1-3 step을 반복한다.
그림으로 표현하면 다음과 같다.
따라서 우리가 찾아야 되는 것은
1) 루트 인덱스
2) 인 오더 리스트에서 왼쪽 서브 트리 탐색 범위와 오른쪽 서브 트리 탐색 범위
3) 포스트 오더 리스트에서 왼쪽 서브 트리 탐색 범위와 오른쪽 서브 트리 탐색 범위
이다. 인 오더 리스트와 포스트 오더 리스트의 탐색 범위가 다른 것은 오른쪽 서브 트리에서 출발하는 경우 끝과 끝을 맞추면서 인덱스에 차이가 발생하기 때문이다.
예를 들어 위의 예시에서 오른쪽 서브 트리를 주목해보자.
인 오더의 경우 탐색 범위를 13 ~ 21로 지정해주어야 되고, 포스트 오더의 경우 12 ~ 20으로 지정해주어야 한다.
루트를 찾은 다음에는 root_index를 기준으로 새로운 탐색 범위를 지정해주어야 한다.
인 오더 리스트 기준으로 왼쪽 서브 트리 탐색 범위는 in_left ~ root_index-1이고 오른쪽 서브 트리는 root_index + 1 ~ in_right 까지이다.
그리고 포스트 오더 리스트 기준으로 왼쪽 서브 트리 탐색 범위는 post_left ~ post_left + root_index-in_left-1이고 오른쪽 서브 트리 탐색 범위는 post_left+root_index-in_left ~ post_right-1까지이다.
따라서 전체적인 작업을 그림으로 표현하면 다음과 같다.
기억할 점
•
트리 순회 비교 문제에서 중요한 점은 루트를 출력한 뒤 서브 트리의 구역들을 재귀 함수로 다시 탐색하는 것이다.