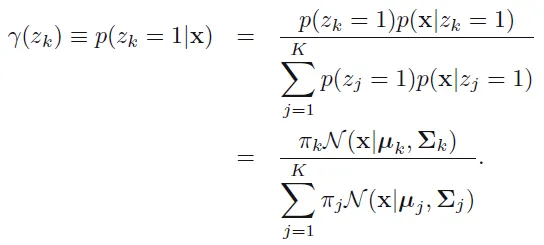////
Search

EM Algorithm

단원
EM
목차

1. 정의

기댓값 최대화(Expectation Maximization) 알고리즘은 관측되지 않은 잠재변수(latent variable)에 의존하는 확률 모델에서 최대가능도(Maximum Likelihood)나 최대사후확률(Maximum a Posteriori)을 갖는 모수(parameter)의 추정값을 찾는 반복적인 알고리즘이다. (출처: 위키백과)
정의를 보면 어려우니 예시를 들어보자.
예를 들어, 두 확률변수 Y1Y_1과 Y2Y_2가 iid로 exponential 분포를 따른다고 가정하자.
Y1,Y2∼iidexp(θ)Y_1, Y_2 \quad \overset{\underset{\mathrm{iid}}{}}{\sim} \quad exp(\theta)
그런데 이 때 y1=5y_1=5가 관측되었고, y2y_2는 관측이 되지 않았다고 하자.(missing) 그럼 이 때 θ\theta의 추정값을 EM 알고리즘을 통해 구할 수 있다.

2. 프로세스

이제 좀 더 구체적으로 EM 알고리즘의 프로세스를 살펴보자.
가장 먼저 용어를 정리하자. 우선, 우리는 확률변수 X로부터 데이터를 관측하였고 (Observed Data from X), 확률변수 Z로부터는 데이터를 관측하지 못했다고 가정한다. (Missing Data from Z)
그리고 X와 Z를 합친 완전한 데이터를 Y = (X, Z)라고 가정한다. 이 때 모수가 주어졌을 때 y의 likelihood function은 다음과 같이 정리할 수 있다.
f(y∣θ)=f(x,z∣θ)=fX(x∣θ)⋅fZ∣X(z∣x,θ)f(y|\theta) = f(x,z|\theta) = f_X(x|\theta) \cdot f_{Z|X}(z|x,\theta)
이 때 양변에 로그를 취하고 x의 log likelihood function을 왼쪽 변으로 몰아서 정리하면 다음을 따른다.
lX(θ)=lY(θ)−log⁡fZ∣X(Z∣X,θ)l_X(\theta) =l_Y(\theta) - \log f_{Z|X}(Z|X,\theta)

E-Step

이제 양변에 Expectation을 취해주자. (with respect to the distribution of Z  ∣  (x,θ(t))Z \; | \; (x,\theta^{(t)}))
E{log⁡fX(x∣θ)  ∣  x,θ(t)}=E{log⁡fY(y∣θ)  ∣  x,θ(t)}−E{log⁡fZ∣X(z∣x,θ)  ∣  x,θ(t)}E\{ \log f_X(x|\theta) \; | \; x,\theta^{(t)} \} = E\{ \log f_Y(y|\theta) \; | \; x,\theta^{(t)} \} - E\{ \log f_{Z|X}(z|x,\theta) \; | \; x,\theta^{(t)} \}
Q(θ  ∣  θ(t))=E{log⁡fY(y∣θ)  ∣  x,θ(t)}Q(\theta \; | \; \theta^{(t)}) = E\{ \log f_Y(y|\theta) \; | \; x,\theta^{(t)} \}, H(θ  ∣  θ(t))=E{log⁡fZ∣X(z∣x,θ)  ∣  x,θ(t)}H(\theta \; | \; \theta^{(t)}) = E\{ \log f_{Z|X}(z|x,\theta) \; | \; x,\theta^{(t)} \} 라고 하자. 그러면,
log⁡fX(x∣θ)=Q(θ  ∣  θ(t))−H(θ  ∣  θ(t))\log f_X(x|\theta) = Q(\theta \; | \; \theta^{(t)}) - H(\theta \; | \; \theta^{(t)})

M-step

위의 식에서 log⁡fX(x∣θ)\log f_X(x|\theta)를 Maximize 하는 것이 우리의 목표라고 했을 때, 우리는 어떤 θ\theta를 골라야할까?
정답은 Q(θ  ∣  θ(t))Q(\theta \; | \; \theta^{(t)})를 θ\theta에 대해 maximize하는 값이다. 그 이유는 H(θ  ∣  θ(t))H(\theta \; | \; \theta^{(t)})는 θ=θ(t)\theta = \theta^{(t)}일 때 최대이기 때문이다.
H(θ(t)  ∣  θ(t))−H(θ  ∣  θ(t))=E{log⁡fZ∣X(Z∣x,θ(t))  ∣  x,θ(t)−log⁡fZ∣X(Z∣x,θ(t))  ∣  x,θ(t)}=∫−log⁡[fZ∣X(z∣x,θ)fZ∣X(z∣x,θ(t))]fZ∣X(z∣x,θ(t))dz≥−log⁡∫fZ∣X(z∣x,θ)dz=0H(\theta^{(t)} \; | \; \theta^{(t)}) - H(\theta \; | \; \theta^{(t)}) \\ = E\{ \log f_{Z|X}(Z|x,\theta^{(t)}) \; | \; x,\theta^{(t)} - \log f_{Z|X}(Z|x,\theta^{(t)}) \; | \; x,\theta^{(t)} \} \\ = \int -\log \left [ \frac{f_{Z|X}(z|x,\theta)}{f_{Z|X}(z|x,\theta^{(t)})} \right ] f_{Z|X}(z|x,\theta^{(t)})dz \\ \ge -\log \int f_{Z|X}(z|x,\theta)dz = 0
∴  H(θ(t)  ∣  θ(t))≥H(θ  ∣  θ(t))\therefore \; H(\theta^{(t)} \; | \; \theta^{(t)}) \ge H(\theta \; | \; \theta^{(t)})
그러므로 θ(t+1)\theta^{(t+1)}을 Q(θ  ∣  θ(t))Q(\theta \; | \; \theta^{(t)})를 maximize 하는 값이라고 하면,
H(θ(t+1)  ∣  θ(t))≥H(θ(t)  ∣  θ(t))H(\theta^{(t+1)} \; | \; \theta^{(t)}) \ge H(\theta^{(t)} \; | \; \theta^{(t)}) 이고 Q(θ(t+1)  ∣  θ(t))≥Q(θ(t)  ∣  θ(t))Q(\theta^{(t+1)} \; | \; \theta^{(t)}) \ge Q(\theta^{(t)} \; | \; \theta^{(t)}) 이므로,
log⁡fX(x∣θ(t+1))≥log⁡fX(x∣θ(t))\log f_X(x|\theta^{(t+1)}) \ge \log f_X(x|\theta^{(t)})
가 성립한다. 따라서 계속해서 θ\theta를 update 하면, global maximum에 가까워질 것이다.

3. 예시

몇 가지 예시를 통해 EM 알고리즘을 이해해보자.

Multinomial Distribution

y=(y1,y2,y3,y4)y = (y_1, y_2, y_3, y_4) 이며 multinomial probability를 가진다고 하자. (12−12θ,14θ,14θ,12)=(p1,p2,p3,p4)(\frac{1}{2}-\frac{1}{2}\theta, \frac{1}{4}\theta, \frac{1}{4}\theta, \frac{1}{2}) = (p_1, p_2, p_3, p_4)
그리고 우리는 관측치 yobs=(y1,y2,y3+y4)=(38,34,125)y_{obs} = (y_1,y_2,y_3+y_4)=(38,34,125)를 가지고 있는 상황이다. 이 때 The Complete-data MLE of θ\theta를 구해보자.
일단, y3y_3과 y4y_4가 따로 구해지지 않고 더한 값이 관측이 되었기 때문에, incomplete data라고 간주할 수 있다.
이 때 complete-data를 yy라고 한다면, yy는 multinomal distribution을 따르기 때문에 log-likelihood function은 다음과 같다.
l(θ)=y1log⁡p1+y2log⁡p2+y3log⁡p3+y4log⁡p4+constantl(\theta) = y_1\log p_1 + y_2\log p_2 + y_3\log p_3 + y_4\log p_4 + constant
이 때 y1,y2,y3,y4y_1, y_2, y_3, y_4 는 sufficient statistics.

1) E-Step

•
Eθ(y1∣yobs)=y1=38E_{\theta}(y_1 | y_{obs}) = y_1 = 38
•
Eθ(y2∣yobs)=y2=34E_{\theta}(y_2 | y_{obs}) = y_2 = 34
•
Eθ(y3∣yobs)=Eθ(y3∣y3+y4)=12514θ12+14θE_{\theta}(y_3 | y_{obs}) = E_{\theta}(y_3 | y_3+y_4) = 125\frac{\frac{1}{4}\theta}{\frac{1}{2}+\frac{1}{4}\theta}
따라서 y3(t)=12514θ(t)12+14θ(t)y^{(t)}_3 = 125\frac{\frac{1}{4}\theta^{(t)}}{\frac{1}{2}+\frac{1}{4}\theta^{(t)}}

2)M-Step

dl(θ)dθ=y11−θ+y2θ+y3θ\frac{dl(\theta)}{d\theta} = \frac{y_1}{1-\theta} + \frac{y_2}{\theta} + \frac{y_3}{\theta}
이므로 dl(θ)dθ=0\frac{dl(\theta)}{d\theta} = 0 으로 두고 θ\theta의 MLE를 구하면,
θ^=y2+y3y1+y2+y3\hat{\theta} = \frac{y_2+y_3}{y_1 + y_2 + y_3}
따라서,
θ(t+1)=34+y3(t)72+y3(t)\theta^{(t+1)} = \frac{34 + y_3^{(t)}}{72 + y_3^{(t)}}

3) Code

이를 R과 Rcpp 코드로 구현해보자.
// [[Rcpp::depends(RcppArmadillo)]] #include <RcppArmadillo.h> using namespace arma; using namespace std; using namespace Rcpp; // Multinomial Example //E-Step NumericVector multi_e(NumericVector x, NumericVector p){ double n1; double n2; double n3; n1 = 38; n2 = 34; n3 = 125*(p[2]/(p[3]+p[2])); NumericVector n = {n1,n2,n3}; return n; } //M-Step NumericVector multi_m(NumericVector n){ double theta = (34+n[2])/(72+n[2]); // 새로운 theta를 구해서 NumericVector p = {1.0/2.0-theta/2, theta/4, theta/4, 1.0/2.0}; // p에 반영 return p; } //Update Iteration // [[Rcpp::export]] NumericVector multi_out(NumericVector x, NumericVector p, int itr){ for(int i = 0; i<itr; i++){ NumericVector n = multi_e(x, p); p = multi_m(n); } return(p); }
C++
복사
#RCPP x = c(38,34,125) n = rep(0,4) theta = 1/2 p = c(1/2-theta/2, theta/4, theta/4, 1/2) itr = 50 multi_out(x,p, itr)
R
복사
[1] 0.1865893 0.1567054 0.1567054 0.5000000
•
50번 Update한 결과
p1=0.1865,p2=0.1567,p3=0.1567,p4=0.5p_1 = 0.1865, p_2 = 0.1567, p_3 = 0.1567, p_4 = 0.5

GMM

GMM의 정의

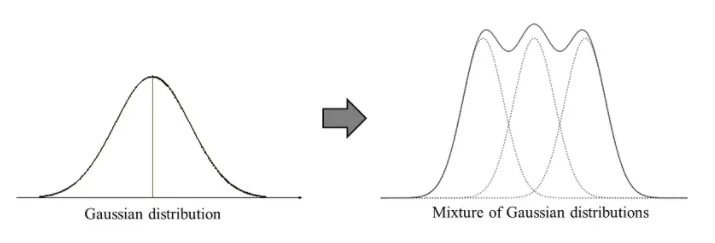
Gaussian Mixture Model(GMM)의 모수를 구하는 데에도 EM 알고리즘이 활용될 수 있다.
Gaussian Mixture Model은 여러 개의 Gaussain 모델이 합쳐진 Clustering 알고리즘이다.
K 개의 Gaussian distribution이 합져져있다고 가정했을 때, Gaussian probability density function은 다음과 같다.
p(X)=∑k=1KπkN(X∣μk,Σk)p(X) = \sum^K_{k=1}\pi_{k}N(X|\mu_k, \Sigma_k)
이 때 πk\pi_k는 k 번 째 Gaussian distribution이 선택될 확률을 나타내며, 따라서 다음을 만족한다.
0≤πk≤10 \le \pi_k \le 1
∑k=1Kπk=1\sum^K_{k=1}\pi_k = 1
결국 우리가 추정하고자 하는 모수는 다음의 세 가지이다.
θ={π,μ,Σ}, where   π={π1,π2,...,πK},  μ={μ1,μ2,...,μK},  Σ={Σ1,Σ2,...,ΣK}\theta = \{ \pi, \mu, \Sigma \}, \\ \text{ where } \; \pi = \{ \pi_1, \pi_2, ..., \pi_K \}, \; \mu = \{ \mu_1, \mu_2, ..., \mu_K \}, \; \Sigma = \{ \Sigma_1, \Sigma_2, ..., \Sigma_K \}

GMM 모수 추정 프로세스

만약 어떤 값들이 주어졌는데, 이 값들이 K개의 Gaussian distribution이 합쳐진 GMM를 따르는 것은 알겠으나, 모수는 모르는 상황이라고 가정하자.
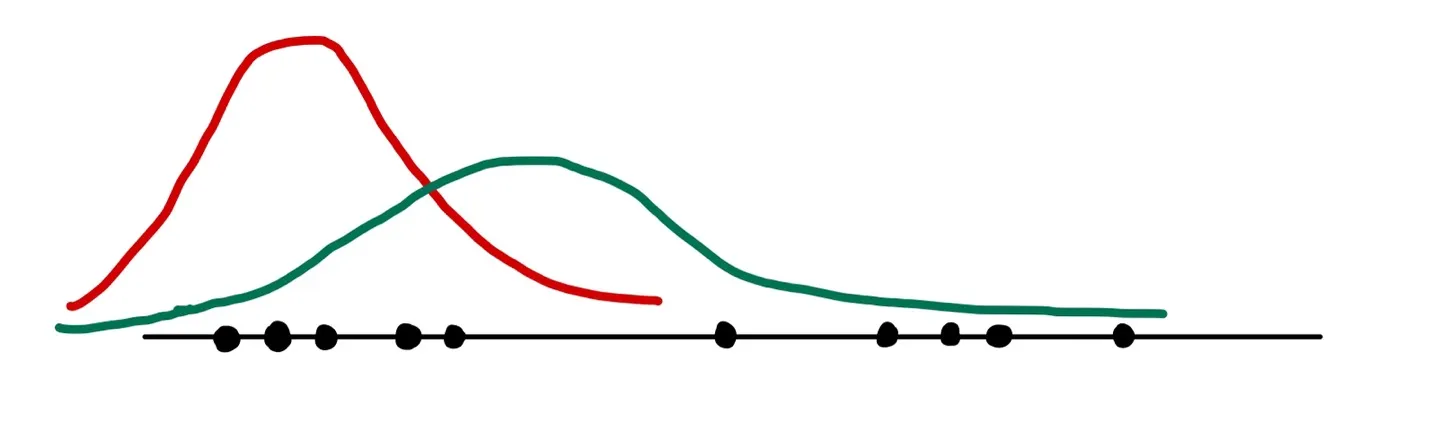
예를 들어, 다음 그림과 같이 2개의 Gaussian distribution이 합쳐진 GMM에서 온 것으로 추정되어지는 값들이 있다고 하자.
그럼 가장 먼저 2개의 평균값과 분산값을 임의로 설정한다.
예를 들어,
μ1=0,Σ1=2.1μ2=2.3,Σ2=5.6\mu_1 = 0, \Sigma_1 = 2.1 \\ \mu_2 = 2.3, \Sigma_2 = 5.6
이라고 하자. 설정된 값들을 가지고 그래프를 그려보면,
이처럼 나올 수 있다.
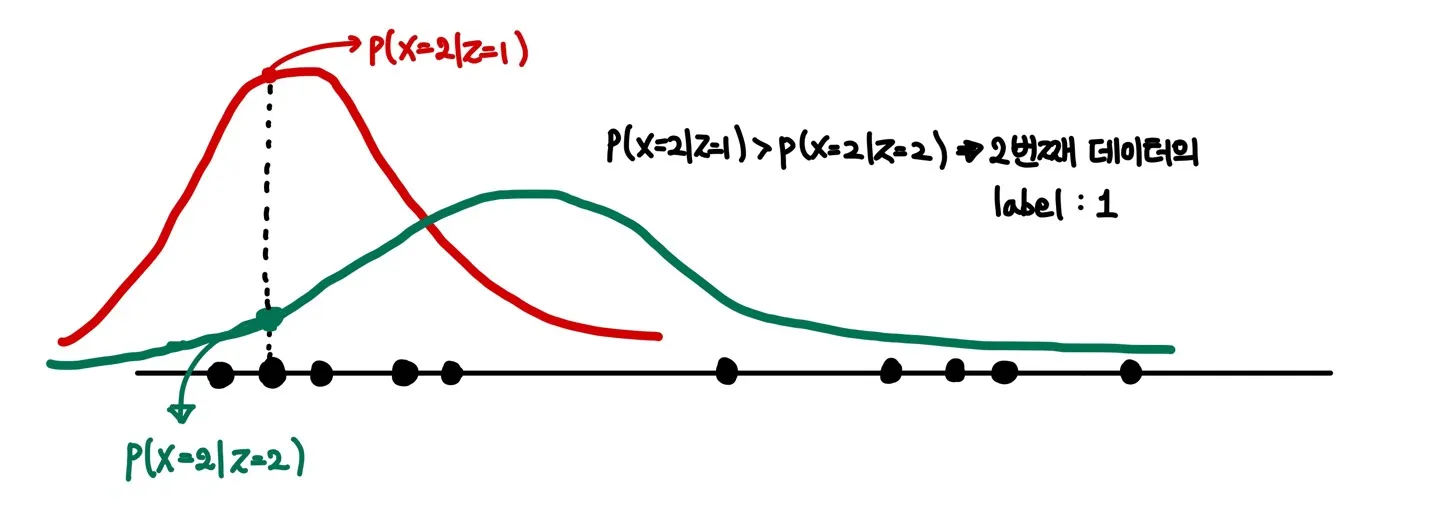
그럼 이제 각각의 데이터들에 대하여 확률값(Likelihood)을 구하고, labeling을 수행해줄 수 있다. 예를 들면, 두 번째 데이터에 대하여 p(x=2∣label=1)p(x = 2 | \text{label} = 1) 과 p(x=2∣label=2)p(x = 2 | \text{label} = 2) 를 비교하여 더 큰 확률값을 가지는 쪽으로 labeling을 수행하는 것.
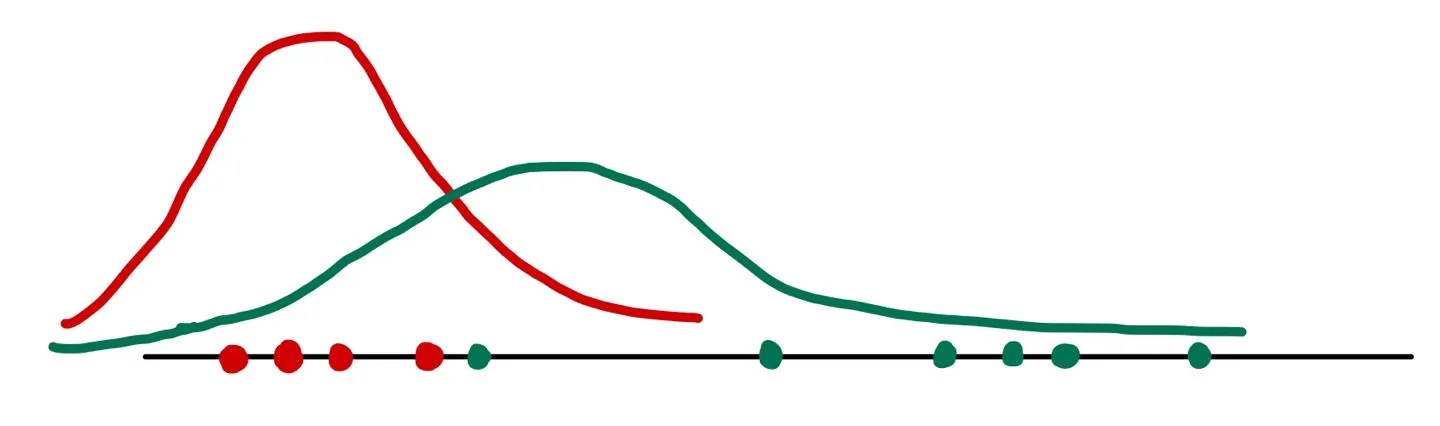
Labeling이 끝난 후에는 labeling된 데이터들을 이용하여 새롭게 모수를 추정한다.
그럼 우리는 새롭게 추정된 모수를 이용하여 다시 labeling을 수행한다. 그리고 이를 반복하면 모수가 수렴할 것이다.
정리하면,
1) K 값 설정
2) 초기 모수값 설정
3) Likelihood 값 기준으로 Labeling
4) 각 그룹별 모수 추정
5) 추정된 모수를 이용하여 분포 제시
6) 수렴할 때까지 3-4 Step 반복

EM 알고리즘 적용

위의 프로세스를 기반으로 EM 알고리즘을 적용해보자.
Z 변수
우선 Latent Variable인 Z=(z1,...zk)Z =(z_1, ...z_k)를 설정하자. 잠재변수 ZZ는 데이터 x가 특정 cluster에서 왔는가를 나타내는 변수이며
p(zk=1)=πk,p(zk=0)=1−πkp(z_k = 1) = \pi_k, \\ p(z_k=0) = 1-\pi_k
라고 정의한다. 즉, 베르누이 분포(Bernoulli distribution)를 따른다.
따라서 ZZ는 시행횟수가 1인 Multinomial Distribution의 형태를 따른다.
p(Z)=p(z1=1)z1p(z2=1)z2...p(zK=1)zK=∏k=1Kπkzkp(Z) = p(z_1 = 1)^{z_1}p(z_2 = 1)^{z_2}...p(z_K = 1)^{z_K} = \prod^K_{k=1}\pi_k^{z_k}
그렇다면, ZZ가 주어졌을 때, 확률변수 X의 분포는 다음과 같이 표현할 수 있다.
p(X∣Z)=∏k=1KN(X∣μk,Σk)zkp(X|Z) = \prod^K_{k=1}\mathcal{N}(X|\mu_k, \Sigma_k)^{z_k}
그러므로, X의 Marginal 분포는 처음에 정의했던 것과 같이 표현될 수 있다.
p(X)=∑Zp(Z)p(X∣Z)=∑k=1KπkN(X∣μk,Σk)p(X) = \sum_Z p(Z)p(X|Z) = \sum^K_{k=1}\pi_k\mathcal{N}(X|\mu_k, \Sigma_k)
E-Step
이제 Z 변수를 활용하여 E-Step을 진행하자.
우선 책임값(responsibility)이라는 것을 정의하자. 책임값은 x\mathbf{x}가 주어졌을 때, zk=1z_k=1일 기댓값을 뜻하며 다음과 같이 표현된다.
γ(zk)≡E(zk=1∣x)\gamma(z_k) \equiv E(z_k=1|\mathbf{x})
그런데 앞에서 zkz_k는 0 또는 1을 갖는 베르누이 분포를 따른다고 정의했으므로
γ(zk)≡E(zk=1∣x)=p(zk=1∣x)\gamma(z_k) \equiv E(z_k=1 |\mathbf{x}) = p(z_k=1|\mathbf{x})
를 만족한다.
베이즈 정리를 이용하여 책임값을 전개하면,
M-Step
앞에서 구한 책임값을 이용하여 M-Step을 진행하자.
우선 확률변수 X의 log-likelihood는 다음과 같다.
l(θ)=ln⁡{∏n=1Np(xn∣θ)}=∑n=1Nln⁡{∑k=1KπkN(xn∣μk,Σk)}l(\theta) = \ln \left \{ \prod^N_{n=1}p(\mathrm{x}_n|\theta) \right \} = \sum^N_{n=1}\ln \left \{ \sum^K_{k=1}\pi_k N(\mathrm{x}_n | \mu_k, \Sigma_k) \right \}
이제 각각의 모수에 대하여 MLE를 구하기 위해 log-likelihood의 편미분 값이 0이 되는 지점을 찾자.
1) μk\mu_k
∂l(θ)∂μk=∑n=1NπkN(xn∣μk,Σk)∑j=1KπjN(xn∣μj,Σj)Σk−1(xn−μk)=0  ⟺  ∑n=1Nγ(znk)(xn−μk)=0\frac{\partial l(\theta)}{\partial \mu_k} = \sum^N_{n=1}\frac{\pi_kN(\mathrm{x}_n | \mu_k, \Sigma_k)}{\sum^K_{j=1}\pi_jN(\mathrm{x}_n | \mu_j, \Sigma_j)}\Sigma^{-1}_k(\mathrm{x}_n - \mu_k) = 0 \\ \iff \sum^N_{n=1}\gamma(z_{nk})(\mathrm{x_n - \mu_k)} =0
∴  μk=∑n=1Nγ(znk)xn∑n=1Nγ(znk)\therefore \; \mu_k = \frac{\sum^N_{n=1}\gamma(z_{nk})\mathrm{x_n}}{\sum^N_{n=1}\gamma(z_{nk})}
2) Σk\Sigma_k
∂l(θ)∂Σk=∑n=1NπkN(xn∣μk,Σk)∑j=1KπjN(xn∣μj,Σj){12Σk−1(xn−μk)(xn−μk)TΣk−1−12Σk−1}=0  ⟺  ∑n=1Nγ(znk){Σk−1(xn−μk)(xn−μk)TΣk−1−1}=0\frac{\partial l(\theta)}{\partial \Sigma_k} = \sum^N_{n=1}\frac{\pi_kN(\mathrm{x}_n | \mu_k, \Sigma_k)}{\sum^K_{j=1}\pi_jN(\mathrm{x}_n | \mu_j, \Sigma_j)} \left \{ \frac{1}{2} \Sigma^{-1}_k(\mathrm{x}_n-\mu_k)(\mathrm{x}_n-\mu_k)^T\Sigma^{-1}_k - \frac{1}{2}\Sigma^{-1}_k \right \} = 0 \\ \iff \sum^N_{n=1}\gamma(z_{nk})\{\Sigma^{-1}_k(\mathrm{x}_n-\mu_k)(\mathrm{x}_n-\mu_k)^T\Sigma^{-1}_k-1\} = 0
∴  Σk=∑n=1Nγ(znk)(xn−μk)(xn−μk)T∑n=1Nγ(znk)\therefore \; \Sigma_k = \frac{\sum^N_{n=1}\gamma(z_{nk})(\mathrm{x}_n-\mu_k)(\mathrm{x}_n-\mu_k)^T}{\sum^N_{n=1}\gamma(z_{nk})}
3) πk\pi_k (mixing coefficient)
mixing coefficient는 앞에서 언급했듯이 0에서 1사이라는 제약조건이 있다. 따라서 라그랑주승수를 이용하자.
Λ(X;θ,λ)=∑n=1Nln⁡∑k=1KπkN(xn∣μk,Σk)+λ(1−∑k=1Kπk)\Lambda(X;\theta, \lambda) = \sum^N_{n=1}\ln \sum^K_{k=1}\pi_kN(\mathrm{x}_n|\mu_k, \Sigma_k) + \lambda(1-\sum^K_{k=1}\pi_k)
∂Λ(X;θ,λ)∂πk=∑n=1NN(xn∣μk,Σk)∑j=1KπjN(xn∣μj,Σj)−λ=0  ⟺  ∑k=1K∑n=1NπkN(xn∣μk,Σk)∑j=1KπjN(xn∣μj,Σj)−λ∑k=1Kπk=0  ⟺  ∑k=1K∑n=1Nγ(znk)−λ=0(∵  ∑k=1Kπk=1)\frac{\partial\Lambda(X;\theta, \lambda)}{\partial\pi_k} = \sum^N_{n=1}\frac{N(\mathrm{x}_n|\mu_k, \Sigma_k)}{\sum^K_{j=1}\pi_jN(\mathrm{x}_n | \mu_j, \Sigma_j)}-\lambda = 0 \\ \iff \sum^K_{k=1}\sum^N_{n=1}\frac{\pi_kN(\mathrm{x}_n|\mu_k, \Sigma_k)}{\sum^K_{j=1}\pi_jN(\mathrm{x}_n | \mu_j, \Sigma_j)} - \lambda\sum^K_{k=1}\pi_k = 0 \\ \iff \sum^K_{k=1}\sum^N_{n=1}\gamma(z_{nk}) - \lambda = 0 \quad (\because \; \sum^K_{k=1}\pi_k=1)
∴  λ=N(∵∑k=1Kγ(znk)=1)\therefore \; \lambda = N \quad (\because \sum^K_{k=1}\gamma(z_{nk})=1)
∂Λ(X;θ,λ)∂πk=∑n=1NN(xn∣μk,Σk)∑j=1KπjN(xn∣μj,Σj)−N=0  ⟺  ∑n=1NπkN(xn∣μk,Σk)∑j=1KπjN(xn∣μj,Σj)−Nπk=0\frac{\partial\Lambda(X;\theta, \lambda)}{\partial\pi_k} = \sum^N_{n=1}\frac{N(\mathrm{x}_n|\mu_k, \Sigma_k)}{\sum^K_{j=1}\pi_jN(\mathrm{x}_n | \mu_j, \Sigma_j)}-N = 0 \\ \iff \sum^N_{n=1}\frac{\pi_kN(\mathrm{x}_n|\mu_k, \Sigma_k)}{\sum^K_{j=1}\pi_jN(\mathrm{x}_n|\mu_j, \Sigma_j)} - N\pi_k = 0
∴  πk=1N∑n=1Nγ(znk)\therefore \; \pi_k = \frac{1}{N}\sum^N_{n=1}\gamma(z_{nk})
정리
EM 알고리즘 Step을 다시 정리하면,
1) μk\mu_k등의 모수들을 모두 초기화 하고 랜덤 값을 부여한다.
2) E-Step: 파라미터들을 고정하고 responsiblity(책임값)을 구한다.
3) M-Step: 2)에서 구한 responsibility로 모수들을 update 한다.
4) log-likelihood로 평가한다.
5) 2-4 Step을 반복한다.