문제
아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.
12 = 5 + 5 + (5 / 5) + (5 / 5)12 = 55 / 5 + 5 / 512 = (55 + 5) / 5
5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.
제한사항
•
N은 1 이상 9 이하입니다.
•
number는 1 이상 32,000 이하입니다.
•
수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.
•
최솟값이 8보다 크면 -1을 return 합니다.
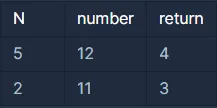
입출력 예시
정답
def solution(N, number):
DP = [] # n번을 사용하여 만들 수 있는 수를 모아놓은 list
for i in range(1, 9):
numbers = set() # DP의 i번째 원소에 담길 수들 / 중복을 허용할 필요가 없으므로 set
numbers.add(int(str(N)*i)) # 단순하게 i개를 이용해서 만들 수 있는 수는 N을 i번 연속해서 쓴 것.
# 이전 set의 조합으로 i번째 set 구하기
for j in range(0, i-1):
for x in DP[j]:
for y in DP[-j-1]:
numbers.add(x+y)
numbers.add(x-y)
numbers.add(x*y)
if y!=0: # 나눗셈이 가능하려면 0이 아니어야 함.
numbers.add(x//y)
# 만약 i번째 원소에 number가 포함된다면 바로 answer를 출력
if number in numbers:
answer = i
return answer
# DP의 i번째 set 추가
DP.append(numbers)
# 끝까지 못 찾으면 -1 출력
return -1
Python
복사
풀이
•
동적 계획법 문제이다.
•
우선 DP라는 리스트를 만들어서 N을 n번 사용하여 만들 수 있는 set을 저장하고 만약에 number가 DP 리스트의 n 번째 원소의 집합 안에 포함된다면 이를 정답으로 출력하게 하자.
•
예를 들어서 DP 리스트의 첫번째 원소에는 집합 {N}이 들어갈 것이고, 만약 number가 N이라면 정답은 1일 것이다.
•
그럼 우리가 해야하는 것은 DP의 원소들을 계속해서 추가하는 것이다.
•
DP의 n 번째 원소를 구하는 방법은 다음과 같다.
•
우선 단순하게 어떤 숫자 N을 n 개 사용하여 만들 수 있는 숫자는 단순하게 N을 n개 늘어놓는 것이다.
•
예를 들어 5를 3개 이용하여 555를 만들 수 있다.
•
따라서 DP의 n 번째 원소에 들어갈 집합을 numbers라고 정의할 때, 가장 먼저 n개를 나열한 값이 포함될 수 있다.
for i in range(1, 9):
numbers = set() # DP의 i번째 원소에 담길 수들 / 중복을 허용할 필요가 없으므로 set
numbers.add(int(str(N)*i)) # 단순하게 i개를 이용해서 만들 수 있는 수는 N을 i번 연속해서 쓴 것.
Python
복사
•
그 다음 가능한 수들의 집합은 다음과 같다.
N을 1번 사용했을 때 SET 과 n-1번 사용했을 때 SET을 사칙연산한 수들의 집합 U
N을 2번 사용했을 때 SET 과 n-2번 사용했을 때 SET을 사칙연산한 수들의 집합 U
... U
N을 n-1번 사용했을 때 SET 과 1번 사용했을 때 SET을 사칙연산한 수들의 집합
•
예를 들어보자.
•
N을 3번 사용해서 만들 수 있는 집합은 (단순 나열 제외)
N을 1번 사용해서 만들 수 있는 집합과 N을 2번 사용해서 만들 수 있는 집합을 사칙연산한 것
U
N을 2번 사용해서 만들 수 있는 집합과 N을 1번 사용해서 만들 수 있는 집합을 사칙연산한 것
이다.
•
실제로 계산으로 표현하면,
◦
N 1번 사용 SET & 사칙연산 & N 2번 사용 SET
▪
5 + (55)
▪
5 + (5+5)
▪
5 + (5-5)
▪
5 + (5//5)
▪
5 + (5*5)
▪
.....
◦
N 2번 사용 SET & 사칙연산 & N 1번 사용 SET
▪
(55) + 5
▪
(5+5) + 5
▪
(5-5) + 5
▪
(5//5) + 5
▪
(5*5) + 5
▪
.....
이런식으로 될 것이다.
따라서 이를 코드로 표현하면 다음과 같다.
# 이전 set의 조합으로 i번째 set 구하기
for j in range(0, i-1):
for x in DP[j]:
for y in DP[-j-1]:
numbers.add(x+y)
numbers.add(x-y)
numbers.add(x*y)
if y!=0: # 나눗셈이 가능하려면 0이 아니어야 함.
numbers.add(x//y)
Python
복사
•
DP의 n번째 원소의 집합인 numbers를 다 구하면 number가 numbers 안에 들어있는지 체크한다. 그리고 들어있다면 바로 answer로 저장하여 출력한다.
# 만약 i번째 원소에 number가 포함된다면 바로 answer를 출력
if number in numbers:
answer = i
return answer
Python
복사
•
만약 포함되어 있지 않다면 계속 검사를 진행해야 하므로 DP에 numbers를 append한다.
# DP의 i번째 set 추가
DP.append(numbers)
Python
복사
•
끝까지 못 찾으면 8번을 사용해서 만들 수 없는 숫자이므로 -1을 출력한다.
# 끝까지 못 찾으면 -1 출력
return -1
Python
복사