////
Search

Romberg Integration

단원
Numerical Integration
목차

1. 정의

일반적으로 Riemann이나, Trapezoidal과 같이 차수가 낮은 뉴턴-코츠 구적법은 converge가 느리다는 단점이 있다. 그래서 이를 보완하기 위하여 Trapezoidal rule estimates를 이용해 적분을 구하는 방식이 Romberg Integration 방법이다.

2. 계산

∫abf(x)dx\int^b_a f(\mathrm{x})d\mathrm{x} 를 동일한 길이인 h=b−anh=\frac{b-a}{n}으로 n개의 subinterval로 나누고 trapezoidal rule을 사용하여 추정한 적분값을 T^(n)\hat{T}(n)이라 하자.
이 때 a=0,b=1a=0, b=1이라고 하자. 그러면 다음이 성립한다.
T^(1)=12f(0)+12f(1),T^(2)=14f(0)+12f(12)+14f(1),T^(4)=18f(0)+14[f(14)+f(24)+f(34)]+18f(1),...\begin{align*} & \hat{T}(1) = \frac{1}{2}f(0) + \frac{1}{2}f(1), \\ & \hat{T}(2) = \frac{1}{4}f(0) + \frac{1}{2}f(\frac{1}{2}) + \frac{1}{4}f(1), \\ & \hat{T}(4) = \frac{1}{8}f(0 ) + \frac{1}{4} \left [ f(\frac{1}{4} ) + f(\frac{2}{4}) + f(\frac{3}{4}) \right ] + \frac{1}{8}f(1), \\ & . \\ & . \\ & . \end{align*}
그런데 위의 수식을 정리해보면,
T^(2)=12T^(1)+12f(12),T^(4)=12T^(2)+14[f(14)+f(34)]\begin{align*} & \hat{T}(2) = \frac{1}{2} \hat{T}(1) + \frac{1}{2}f(\frac{1}{2}), \\ & \hat{T}(4) = \frac{1}{2} \hat{T}(2) + \frac{1}{4} \left [ f(\frac{1}{4}) + f(\frac{3}{4}) \right ] \end{align*}
임을 알 수 있다. 이를 일반화하면,
T^(2n)=12T^(n)+h2∑i=1nf(a+(i−12)h)\hat{T}(2n) = \frac{1}{2}\hat{T}(n) + \frac{h}{2}\sum^n_{i=1}f \left(a + (i-\frac{1}{2})h \right)
로 정리할 수 있다.
따라서 T^i,0=T^(2i)\hat{T}_{i,0} = \hat{T}(2^i) 라고 정의했을 때, j=1,...,ij=1,..., i 와 i=1,...,mi = 1,...,m에 대하여 다음이 성립한다.
T^i,j=4jT^i,j−1−T^i−1,j−14j−1\hat{T}_{i,j} = \frac{4^j\hat{T}_{i,j-1}-\hat{T}_{i-1,j-1}}{4^j-1}
이를 이용하여 다음과 같은 추정치의 삼각형 배열 형태를 만들 수 있다.
T^0,0T^1,0T^1,1T^2,0T^2,1T^2,2T^3,0T^3,1T^3,2T^3,3T^4,0T^4,1T^4,2T^4,3T^4,4    ⋮  ⋮  ⋮  ⋮  ⋮  ⋱\begin{align*} & \hat{T}_{0,0} \\ & \hat{T}_{1,0} \quad \hat{T}_{1,1} \\ & \hat{T}_{2,0} \quad \hat{T}_{2,1} \quad \hat{T}_{2,2} \\ & \hat{T}_{3,0} \quad \hat{T}_{3,1} \quad \hat{T}_{3,2} \quad \hat{T}_{3,3} \\ & \hat{T}_{4,0} \quad \hat{T}_{4,1} \quad \hat{T}_{4,2} \quad \hat{T}_{4,3} \quad \hat{T}_{4,4} \\ & \;\; \vdots \; \qquad \vdots \;\qquad \vdots \;\qquad \vdots \;\qquad \vdots \;\qquad \ddots \end{align*}
이제 남은 것은 적절한 T^i,j\hat{T}_{i,j}를 고르는 일이다. 이 때 기준은 두 가지이다.
•
Numerical Approximation Error
•
Computer Roundoff Error

Errors

Numerical Approximation Error는 수치적분 방법 자체에서 오는 Error를 의미한다. 수치적분 방법은 적분 구간을 쪼개서 근사적으로 적분값을 구하는 방식이기 때문에 앞선 포스트들에서 살펴보았듯이 실제 적분값과 오차가 발생한다. 이러한 오차는 구간을 더 잘게 쪼개면(n을 늘리는 것) 줄어든다(무조건적으로 줄어들지는 않고 커브를 그린다). 그러나 Efficiency의 관점에서 더 잘게 쪼개는 것이 그다지 이익이 없을 때, 즉, n을 높이더라도 큰 차이가 없을 때엔 n을 높이는 것을 중단한다.
Romberg Integration에서 이를 판단하는 기준은 T^i,j−T^i−1,j\hat{T}_{i,j} - \hat{T}_{i-1,j} 이다. 이 값이 충분히 작다면 T^i,j\hat{T}_{i,j}를 선택한다.
그런데, 우리는 또다른 Error를 고려해야한다. 바로 반올림에 관한 Error이다. T^i,j\hat{T}_{i,j}값들이 깔끔하게 떨어지면 좋겠지만, 그렇지 못한 경우가 대부분이며 computer에서는 계산을 위해 반올림을 수행할 수밖에 없다. 따라서 계산을 진행함에 따라 반올림에 대한 Error가 누적된다. 이를 Computer Roundoff Error라고 부른다. Computer Roundoff Error가 적은지는 다음의 값을 통해 살펴본다.
Qij=T^i,j−T^i−1,jT^i+1,j−T^i,jQ_{ij} = \frac{\hat{T}_{i,j}-\hat{T}_{i-1,j}}{\hat{T}_{i+1,j}-\hat{T}_{i,j}}
Numerical approximation error가 Computer roundoff error보다 훨씬 큰 경우에는 QijQ_{ij} 값은 ii값이 증가할수록 4j+14^{j+1}에 가까워진다. 그런데, 반대로 computer roundoff error가 훨씬 더 큰 경우 QijQ_{ij}값은 불규칙한 값을 나타낸다. (음수가 나오거나 엄청 크거나 작은 값이 나오거나)
따라서,
•
첫 번째로 T^i,j−T^i−1,j\hat{T}_{i,j} - \hat{T}_{i-1,j} 값으로 numerical approximation error가 충분히 작은지를 판단하고
•
두 번째로 QijQ_{ij}값이 4j+14^{j+1}에 가까운지를 확인하여(가깝다면 computer roundoff error도 작다는 의미)
T^i,j\hat{T}_{i,j}를 고르면 된다.

3. 활용 및 Code

문제를 통해 Romberg Integration을 한번 활용해보자.
X∼Unif[1,5]X \sim \text{Unif}[1,5] 이고 Y=4/XY = 4/X 라고 하자. 이때 E[Y]=log⁡5E[Y] = \log 5를 Romberg Integration을 통해 구해보자. 단, m = 10으로 설정한다.
우선 E[Y]=log⁡5E[Y] = \log 5 가 되는 것부터 알아보자.
일차함수 변환을 이용하면,
f(y)=1y2,45≤y≤4f(y) = \frac{1}{y^2}, \quad \frac{4}{5} \le y \le 4
임을 알 수 있다. 따라서,
E[Y]=∫454y⋅1y2dy=∫4541ydy=log⁡4−log⁡45=log⁡4−log⁡4+log⁡5=log⁡5E[Y] = \int^4_{\frac{4}{5}}y\cdot\frac{1}{y^2}dy=\int^4_{\frac{4}{5}}\frac{1}{y}dy=\log4-\log{\frac{4}{5}}=\log4-\log4+\log5=\log5
그럼 이때 log⁡y\log y의 미분값이 1y\frac{1}{y}라는 것을 모른다고 가정했을 때 ∫4541ydy\int^4_{\frac{4}{5}}\frac{1}{y}dy를 계산해보자.
R과 Rcpp를 이용하여 코드를 작성하였다.
우선 f 함수와 ∑i=1nf(a+(i−12)h)\sum^n_{i=1}f \left(a + (i-\frac{1}{2})h \right)를 Rcpp 함수로 작성하였다.
double fy(double y){ return 1/y; } double fy_sum(int n){ double s = 0; double h = 3.2/n; for(int i = 1; i < n+1; i++){ s = s + fy(0.8 + (i-0.5)*h); } return s; }
C++
복사
그 다음 Triangle Estimates를 matrix 형식으로 저장하여 출력하는 함수를 작성하였다.
// [[Rcpp::export]] mat triangle_y(int m){ mat T(m, m-1); T(0,0) = 0.5*(fy(0.8)+fy(4)); for(int i = 1; i < m; i++){ T(i,0) = 0.5 * T(i-1,0) + fy_sum(pow(2, i-1))*(3.2)/pow(2.0,i); for(int j = 1; j < i; j++){ T(i,j) = ( pow(4,j)*T(i,j-1) - T(i-1,j-1) ) / ( pow(4,j) -1 ); } } return T; }
C++
복사
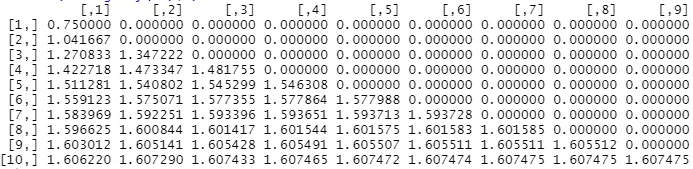
이제 R로 함수를 불러와 m = 10으로 설정하여 출력하면 다음과 같은 결과를 얻는다.
round(triangle_y(10),7)
R
복사
점점 True 값인 log⁡5≈1.609438\log 5 \approx 1.609438 에 가까워지는 것을 확인할 수 있다.