////
Search

트리 지름 구하기

출처: https://blog.myungwoo.kr/112
목차

1. 트리의 지름

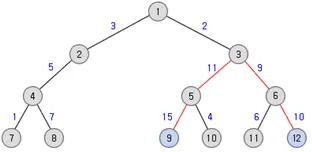
트리의 지름이란 가장 먼 두 정점 사이의 거리 또는 가장 먼 두 정점을 연결하는 경로를 의미한다. 이때 부모와 자식 노드 사이의 거리를 1로 볼 수도 있고 가중치를 주어 부모와 자식 노드 사이의 거리를 1 이상으로 만들 수도 있다.
ex) 가중치가 주어진 트리

2. 트리 지름 구하기 알고리즘

트리의 지름을 구하는 알고리즘은 다음과 같다.
1.
임의의 점(노드) xx를 잡는다.
2.
xx에서 가장 거리가 먼 점 yy를 잡는다.
3.
yy에서 가장 거리가 먼 점 zz를 잡는다.
4.
yy와 zz간의 경로가 트리의 지름이다.

증명

트리에서 정점 uu와 vv를 연결하는 경로가 지름이라고 가정하자.
그리고 위의 알고리즘에서 2번까지 시행했다고 하자. 즉, 임의의 점 xx를 잡고 xx에서 가장 먼 점 yy를 잡았다고 하자.
이때 가능한 모든 경우는 다음과 같다.
1) xx가 uu 또는 vv인 경우
2) yy가 uu 또는 vv인 경우
3) x,y,u,vx, y, u, v가 모두 다른 점인 경우

xx가 uu 또는 vv인 경우

우선 x=ux=u라고 하자.
이때 d(x,y)≤d(u,v)d(x,y) \le d(u,v)이다. 왜냐하면 u−vu -v는 지름이기 때문에 가장 크기 때문이다. 따라서 xx에서 가장 먼 점을 잡으려면 yy를 vv로 잡으면 된다.
그리고 마찬가지로 d(y,z)≤d(u,v)d(y,z) \le d(u,v)이기 때문에 yy에서 가장 먼 점을 잡으려면 zz를 u(=x)u(=x)로 잡으면 된다.
따라서 d(z,y)=d(u,v)d(z,y) = d(u,v) 이므로 z−y z-y는 트리의 지름이 된다.
x=vx=v 인 경우는 동일한 방식으로 d(z,y)=d(u,v)d(z,y) = d(u,v)를 만족하게 된다.

yy가 uu 또는 vv인 경우

yy가 uu인 경우는 x=vx=v인 경우와 동일해지고, yy가 vv인 경우는 x=ux=u인 경우와 동일해진다. 따라서 두 경우 모두 알고리즘을 만족한다.

x,y,u,vx, y, u, v가 모두 다른 점인 경우

이 경우엔 두 가지 경우로 나눌 수 있다.
1) x−yx-y와 u−vu-v 경로가 모두 정점 tt를 지나는 경우
2) x−yx-y와 u−vu-v 경로가 완전히 독립인 경우
1) 부터 살펴보자.
이때 d(t,y)=max⁡(d(u,t),d(t,v))d(t,y) =\max(d(u,t), d(t,v))를 무조건 만족한다. 증명은 다음과 같다.
일단 max⁡(d(u,t),d(t,v))=d(t,v)\max(d(u,t), d(t,v)) = d(t,v) 라고 하자.
(1) d(t,y)<max⁡(d(u,t),d(t,v))=d(t,v)d(t,y) <\max(d(u,t), d(t,v)) = d(t,v)
인 경우 xx에서 가장 먼 점은 yy가 아니라 vv이다. (∵d(x,t)+d(t,v)>d(x,t)+d(t,y)\because d(x,t) +d(t,v) > d(x,t) + d(t,y))
따라서 모순
(2) d(t,y)>max⁡(d(u,t),d(t,v))=d(t,v)d(t,y) > \max(d(u,t), d(t,v)) = d(t,v)
인 경우 d(u,v)<d(x,y)d(u,v) < d(x,y) 가 되어 u−vu-v가 트리의 지름이라는 가정에 모순된다.
이제 zz를 잡는데 zz를 잡을 때도 두 가지의 경우로 나뉜다.
(1) yy와 zz 경로 사이에 tt가 없는 경우
(2) yy와 zz 경로 사이에 tt가 있는 경우
(1) yy와 zz 경로 사이에 tt가 없는 경우
만약 d(y,z)<d(u,v)d(y,z) < d(u,v)라고 하자.
그런데 d(y,v)=2(t,v)≥d(u,v)d(y,v) = 2(t,v) \ge d(u,v) 이므로 zz는 yy에서 가장 먼 점이라는 가정에 모순된다.
따라서 d(y,z)≥d(u,v)d(y,z) \ge d(u,v) 이므로 알고리즘을 만족한다.
(2) yy와 zz 경로 사이에 tt가 있는 경우
d(y,z)=d(t,y)+d(t,z)≤d(u,v)=d(u,t)+d(t,v)d(y,z) = d(t,y) + d(t,z) \le d(u,v) = d(u,t)+d(t,v)
d(t,y)=d(t,v)d(t,y) = d(t,v) 이므로 d(t,z)≤d(u,t)d(t,z) \le d(u,t)
d(t,z)<d(u,t)d(t,z) < d(u,t) 라면 zz는 yy의 가장 먼 점이 아니다. 왜냐하면 z=uz=u로 잡으면 더 멀기 때문이다. 따라서 d(t,z)=d(u,t)d(t,z) = d(u,t) 그러므로 d(y,z)=d(u,v)d(y,z) = d(u,v)
이제 경로들이 완전히 독립인 경우를 살펴보자.
2)
xx에서 가장 먼 점이 yy이기 때문에 d(t,y)>max⁡(d(u,t),d(v,t))d(t,y) > \max(d(u,t), d(v,t))이다.
그런데 이는 uu에서 vv보다 uu에서 yy가 더 멀다는 것을 의미한다. d(t,y)>d(v,t)=d(t,s)+d(s,v)d(t,y) > d(v,t) = d(t,s) + d(s,v) 이므로 d(u,y)=d(u,s)+d(s,t)+d(t,y)>d(u,s)+d(s,v)=d(u,v)d(u,y) = d(u,s)+d(s,t) +d(t,y) > d(u,s) + d(s,v)=d(u,v)
따라서 u−vu-v가 트리의 지름이라는 가정에 모순된다.