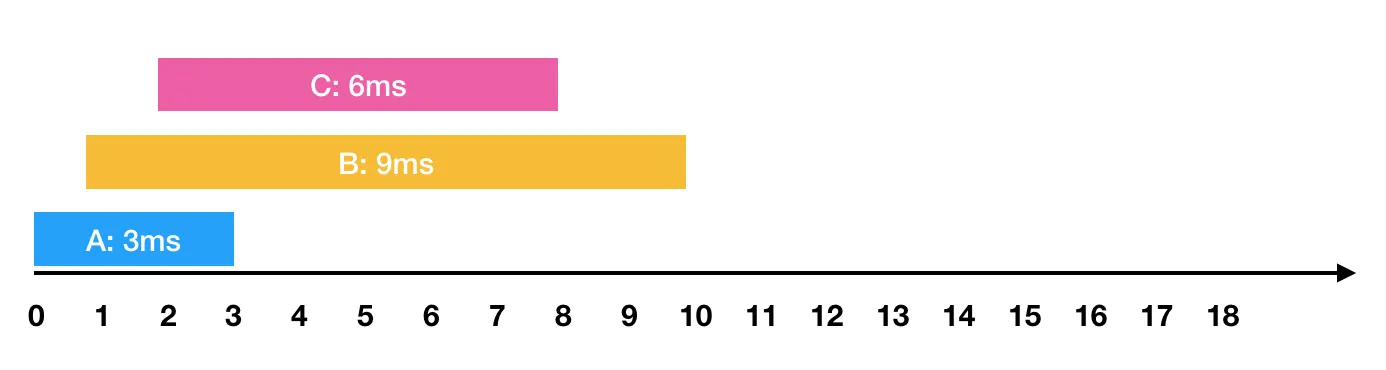문제
하드디스크는 한 번에 하나의 작업만 수행할 수 있습니다. 디스크 컨트롤러를 구현하는 방법은 여러 가지가 있습니다. 가장 일반적인 방법은 요청이 들어온 순서대로 처리하는 것입니다.
예를들어
- 0ms 시점에 3ms가 소요되는 A작업 요청
- 1ms 시점에 9ms가 소요되는 B작업 요청
- 2ms 시점에 6ms가 소요되는 C작업 요청
Plain Text
복사
와 같은 요청이 들어왔습니다. 이를 그림으로 표현하면 아래와 같습니다.
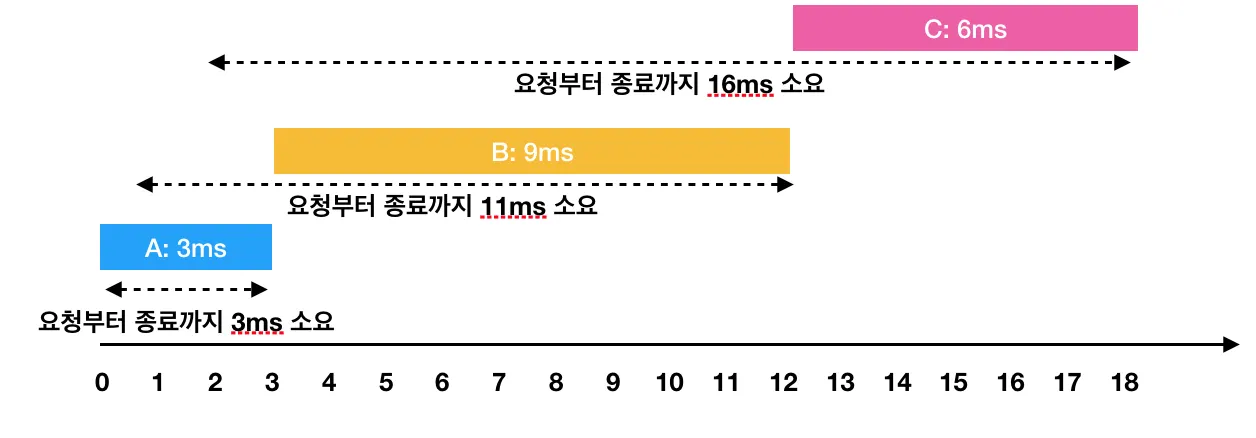
한 번에 하나의 요청만을 수행할 수 있기 때문에 각각의 작업을 요청받은 순서대로 처리하면 다음과 같이 처리 됩니다.
- A: 3ms 시점에 작업 완료 (요청에서 종료까지 : 3ms)
- B: 1ms부터 대기하다가, 3ms 시점에 작업을 시작해서 12ms 시점에 작업 완료(요청에서 종료까지 : 11ms)
- C: 2ms부터 대기하다가, 12ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 16ms)
Plain Text
복사
이 때 각 작업의 요청부터 종료까지 걸린 시간의 평균은 10ms(= (3 + 11 + 16) / 3)가 됩니다.
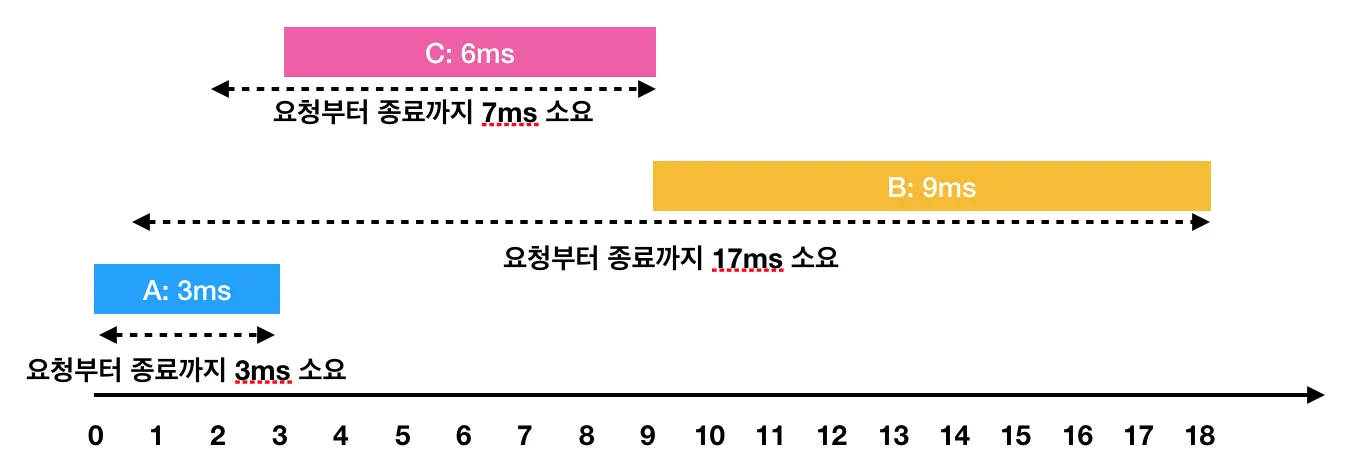
하지만 A → C → B 순서대로 처리하면
- A: 3ms 시점에 작업 완료(요청에서 종료까지 : 3ms)
- C: 2ms부터 대기하다가, 3ms 시점에 작업을 시작해서 9ms 시점에 작업 완료(요청에서 종료까지 : 7ms)
- B: 1ms부터 대기하다가, 9ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 17ms)
Plain Text
복사
이렇게 A → C → B의 순서로 처리하면 각 작업의 요청부터 종료까지 걸린 시간의 평균은 9ms(= (3 + 7 + 17) / 3)가 됩니다.
각 작업에 대해 [작업이 요청되는 시점, 작업의 소요시간]을 담은 2차원 배열 jobs가 매개변수로 주어질 때, 작업의 요청부터 종료까지 걸린 시간의 평균을 가장 줄이는 방법으로 처리하면 평균이 얼마가 되는지 return 하도록 solution 함수를 작성해주세요. (단, 소수점 이하의 수는 버립니다)
제한 사항
•
jobs의 길이는 1 이상 500 이하입니다.
•
jobs의 각 행은 하나의 작업에 대한 [작업이 요청되는 시점, 작업의 소요시간] 입니다.
•
각 작업에 대해 작업이 요청되는 시간은 0 이상 1,000 이하입니다.
•
각 작업에 대해 작업의 소요시간은 1 이상 1,000 이하입니다.
•
하드디스크가 작업을 수행하고 있지 않을 때에는 먼저 요청이 들어온 작업부터 처리합니다.
입출력 예시
정답
import heapq
def solution(jobs):
answer = 0
end = 0
i = 0
start = -1
hq = []
while i < len(jobs):
for job in jobs: #job들에 대하여
if start<job[0]<=end: # 시작보다 크거나 end보다 작거나 같은 값들을 힙에 추가
heapq.heappush(hq, [job[1], job[0]])
if len(hq) > 0: # 처리해야 할 일이 있다면
current = heapq.heappop(hq) # 가장 먼저 처리해야 할 일 pop
start = end # start 시간은 end 시간으로 대체
end += current[0] # end 시간은 현재 end 시간에 소요시간을 더한것
answer += end-current[1] # 총 소요시간 += (현재 소요시간 + 대기시간) = (현재 소요시간 + 이전 end - 작업요청시점) = (현재 end - 작업요청시점)
i += 1 # 한 개 처리 될 때 마다 += 1
else:
end += 1 # 탐색되는 job이 없으면 end를 1씩 늘려봄.
return answer//len(jobs)
Python
복사
풀이
•
평균 시간을 가장 빨리 줄이고 싶다면 현재 들어와있는 일 중에 제일 빨리 끝나는 것을 선택하면 된다.
•
조금 변형된 Activity Selection Problem 같다.
•
우선 필요한 parameter는 end와 start이다. 우리는 현재 처리하고 있는 일의 시작과 끝 사이에 어떤 작업들이 들어오는지를 확인해야 한다. 따라서 start는 현재 처리하고 있는 일의 시작이고 end는 현재 작업하고 있는 일의 끝 시간이다.
answer = 0
end = 0
start = -1
i = 0
hq = []
Python
복사
•
그 다음 현재 처리하고 있는 작업의 작업 시간 사이에 들어온 작업들을 힙 자료구조에 넣는다.
•
힙 자료구조에 넣는 이유는 작업소요시간이 제일 짧은 것이 가장 앞에 오도록 하기 위함이다.
•
모든 작업이 처리될 수 있도록 하나의 작업이 처리되면 i가 하나씩 오르도록 하고 while문을 사용하여 작업 갯수에 다다를 때까지 작업을 돌린다.
while i < len(jobs):
Python
복사
•
jobs 내의 모든 작업들에 대해 현재 작업하는 일의 시작시간보다 요청 시간이 크고 마치는 시간보다 작거나 같은 모든 작업들을 힙 자료구조에 넣는다. 이때 기준은 소요시간이 짧을 수록 그리고 요청 시간이 빠를수록 앞으로 오도록 한다.
for job in jobs: #job들에 대하여
if start<job[0]<=end: # 시작보다 크거나 end보다 작거나 같은 값들을 힙에 추가
heapq.heappush(hq, [job[1], job[0]]) # 소요시간을 기준으로 push
Python
복사
•
만약 현재 힙 자료구조에 작업이 남아있다면 가장 먼저 처리해야 할 일을 우선 pop한다.
if len(hq) > 0: # 처리해야 할 일이 있다면
current = heapq.heappop(hq) # 가장 먼저 처리해야 할 일 pop
Python
복사
•
그러고 나서 start는 현재 end 시간으로 대체하고 end 시간은 이제 처리해야 하는 작업의 총 소요시간을 더해준다.
start = end # start 시간은 end 시간으로 대체
end += current[0] # end 시간은 현재 end 시간에 소요시간을 더한것
Python
복사
•
그리고 총 소요시간은 이제 소요될 시간에 그동안 대기했던 시간을 더한 값을 더해주면 된다.
•
그런데 대기시간은 이전의 end 시간에서 작업 요청 시간을 뺀 값이다.
•
따라서 수식으로 표현하면 (현재 소요시간 + 대기시간) = (현재 소요시간 + 이전 end - 작업요청시점)이다. 그런데 현재 소요시간 + 이전 end 시간은 이제 현재 end 시간이므로 (현재 소요시간 + 대기시간) = (현재 end - 작업요청시점) 으로 표현할 수 있다.
answer += end-current[1] # 총 소요시간 += (현재 소요시간 + 대기시간) = (현재 소요시간 + 이전 end - 작업요청시점) = (현재 end - 작업요청시점)
Python
복사
•
한 개가 처리됐으면 i += 1
i += 1 # 한 개 처리 될 때 마다 += 1
Python
복사
•
만약 현재 들어온 작업이 없으면 end 시간을 늘려서 job을 검색해본다.
else:
end += 1 # 탐색되는 job이 없으면 end를 1씩 늘려봄.
Python
복사
•
평균 시간을 구해야 하므로 마지막에 작업의 개수로 총 소요시간을 나눠준다.
return answer//len(jobs)
Python
복사