Hill-Climbing Search

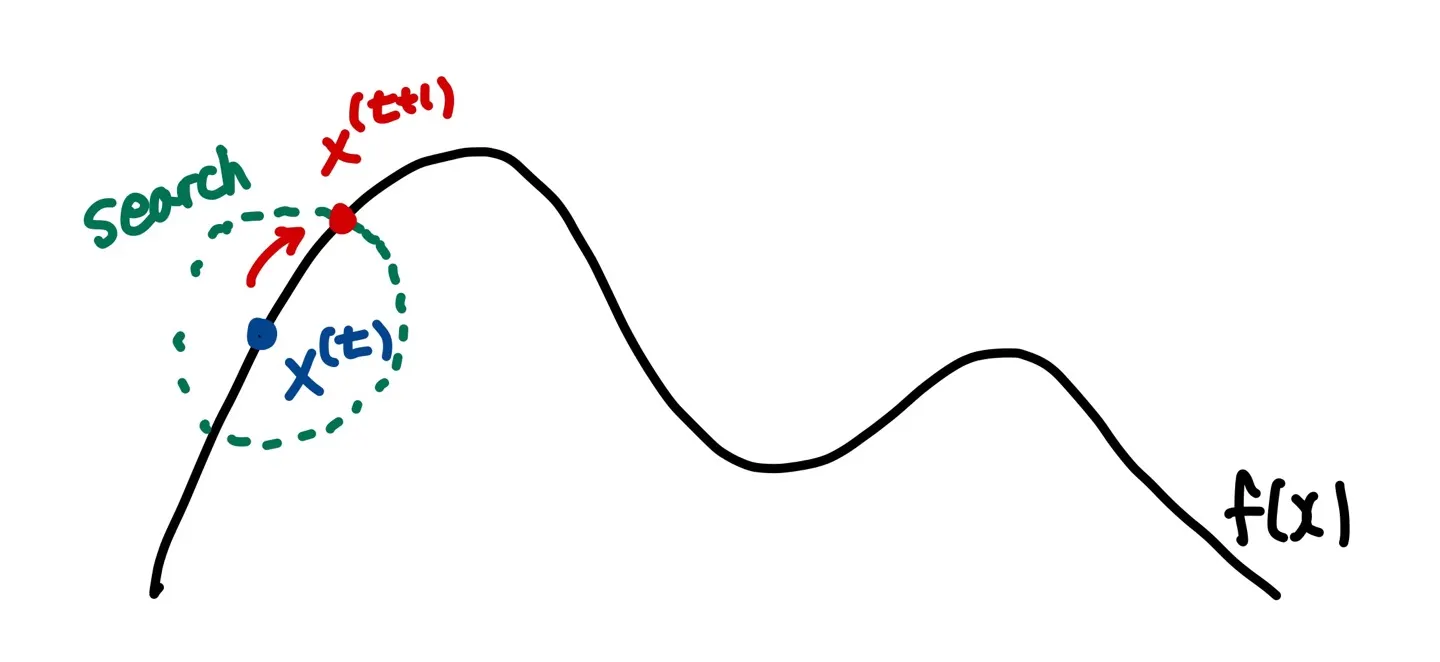
언덕 오르기 탐색(Hill-Climbing Search)은 주변 값을 탐색하여 점차적으로 좋은 값으로 올라간다는 점에서 그 이름이 붙여졌다. 현재 위치에서 주변 값을 탐색하여 후보 값들을 선정한 뒤 그 중에서 하나를 골라서(제일 좋은 것을 고를 수도 있고 랜덤으로 하나를 고를 수도 있다.) 값을 점차적으로 update 하는 방식이다.

Hill-Climbing Search는 대표적인 Local Search Algorithm으로, 전체를 한번에 탐색하는 것이 아니라, 주변(local)을 계속해서 탐색하면서 optimum 값을 찾아가는 방식이다.

2. Update Step

Hill-Climbing Search를 위해서는 두 가지를 설정해주어야 한다.

Neighborhood

우리는 우선 주변값을 정의해주어야 한다. 우리는 현재 위치에서 주변값을 탐색하고, 그 주변값들을 다음 update의 후보값(candidate solution)으로 선정하여 후보값과 현재값을 비교해서 update를 진행한다. 따라서 우리는 무엇을 주변값 또는 이웃값(Neighborhood)으로 설정할 것인지를 우선 정의해야 한다.

목적함수(Objective Function)

후보값을 선정한 다음에는 후보값과 현재값을 비교해야 한다. 그때 평가의 기준이 되는 것이 목적함수이다. 목적함수에 후보값과 현재값을 각각 넣어 평가치를 계산하고 그 평가치를 기준으로 다음 값을 결정한다.

Iteration Step

시작점(Starting Point, θ(0)\theta^{(0)}θ(0)) 설정

Neighborhood(N(θ(t))\mathcal{N}(\theta^{(t)})N(θ(t)))를 Search 해서 후보값들 중 목적함수의 값이 가장 좋은 값을 선택(θ∗\theta^{*}θ∗)

f(θ∗)f(\theta^*)f(θ∗)와 f(θ(t))f(\theta^{(t)})f(θ(t)) 값 비교

f(θ(t+1))=max⁡(f(θ∗),f(θ(t)))f(\theta^{(t+1)}) = \max (f(\theta^*), f(\theta^{(t)}))f(θ(t+1))=max(f(θ∗),f(θ(t))) 로 update

step 2-4 를 iteration 만큼 반복

3. 장단점

장점

•

메모리 사용량이 적다.

•

무한하거나 아주 큰 공간에서 합리적인 해를 찾아낼 수 있다.

단점

•

local optimum에 빠질 수 있다.

•

주변값과 현재값이 동일하다면 이동을 멈출 수 있다.

4. 대안

Hill-Climbing Search의 단점들을 보완하기 위해 여러 대안들이 제시되었다.

Stochastic Climbing

•

최적의 Neighborhood를 선택하는 것이 아니라 current value(θ(t)\theta^{(t)}θ(t))보다 나은 Neighbor 중 하나를 임의로 선택하는 방식.

First-Choice Climbing(Random Ascent)

•

neighbor들을 전부 찾고나서 비교하는 것이 아니라, neighbor를 찾을 때마다 current value와 비교해서 더 나은 값이 나오면 바로 선택하는 방식.

Random Start

•

시작점에 따라서 결과가 달라질 수 있기 때문에 시작점을 여러 개 설정하고 결과를 종합하여 결과를 선택하는 방식.

5. Code 및 활용

Hill-Climbing Search는 MLE 등 다양한 최적화 문제에서 활용될 수 있다. 그리고 Variable Selection에도 활용할 수 있다. Regression에서 Predictor Variable의 수가 많아질 때 우리는 어떤 Variable 조합이 최선인지를 밝혀내야 한다. 이때 만약 단순히 모든 조합들을 단순 비교한다고 하면 매우 비효율적이다. 왜냐하면 n개의 Predictor Variable이 존재할 때 가능한 모든 조합의 수는

2^{n+1}-1

이기 때문이다. 따라서 Hill-Climbing Search를 활용해서 Variable Selection을 진행해보자.

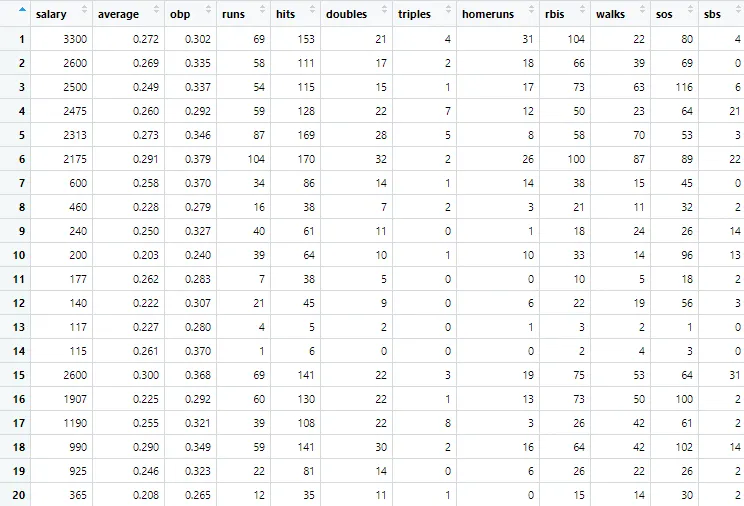
Data: Baseball Salaries

•

337명의 야구선수에 대하여 그들의 1991년의 27개의 baseball performance statistics와 1992년의 salary 정보 데이터가 있다.

•

1991년도 27개의 baseball performance statistics를 predictor variable로, 1992년의 salary를 response variable로 설정하여 어떤 performance statistics들이 salary를 가장 잘 설명하는지를 밝혀내보자.

기본 셋팅

•

Neighborhood는 1-Change 방식으로, 현재의 변수 조합에서 변수 하나를 추가하거나 하나를 제외한 조합을 neighbor로 간주한다.

•

목적함수는 -AIC로 설정한다.

•

Random Start 방식을 도입한다.

Code

1) Hill-Climbing Search(Steepest Ascent)

R을 사용하여 구현하였다.

## INITIAL VALUES
baseball.dat = read.table('baseball.dat',header=TRUE)
baseball.dat$freeagent = factor(baseball.dat$freeagent)
baseball.dat$arbitration = factor(baseball.dat$arbitration)
baseball.sub = baseball.dat[,-1]
salary.log = log(baseball.dat$salary)
n = length(salary.log) #case 개수
m = length(baseball.sub[1,]) #독립변수 개수
num.starts = 5 #random start 개수
runs = matrix(0,num.starts,m)
itr = 15
runs.aic = matrix(0,num.starts,itr)

# INITIALIZES STARTING RUNS
set.seed(1234) 
for(i in 1:num.starts){runs[i,] = rbinom(m,1,.5)} 
#random으로 열을 뽑는 것을 다섯 번 시행


## MAIN
for(k in 1:num.starts){
	run.current = runs[k,]

	# ITERATES EACH RANDOM START
	for(j in 1:itr){
		run.vars = baseball.sub[,run.current==1] #1로 선택된 변수들 뽑아내기.
		g = lm(salary.log~.,run.vars)
		run.aic = extractAIC(g)[2] #[1]은 equivalent d.f, [2]가 AIC
		run.next = run.current

		# TESTS ALL MODELS IN THE 1-NEIGHBORHOOD AND SELECTS THE
		# MODEL WITH THE LOWEST AIC
		for(i in 1:m){
			run.step = run.current
			run.step[i] = !run.current[i] #0이라면 1로 1이라면 0으로 바꿈.
			run.vars = baseball.sub[,run.step==1] #바뀐 것으로 variable을 새로 뽑음.
			g = lm(salary.log~.,run.vars) #model 적용
			run.step.aic = extractAIC(g)[2] #AIC 구하기
			if(run.step.aic < run.aic){
				run.next = run.step
				run.aic = run.step.aic
			} #만약 AIC가 더 작다면 run.next로 할당해줌. 그리고 run.aic도 바꿔줌
		}
		run.current = run.next #run.next를 current에 적용.
		runs.aic[k,j]=run.aic 
	}
	runs[k,] = run.current #최종적으로 제일 작은 aic를 가진 subset이 골라짐.
}

## OUTPUT
runs 		# LISTS OF PREDICTORS
runs.aic 	# AIC VALUES
R
복사

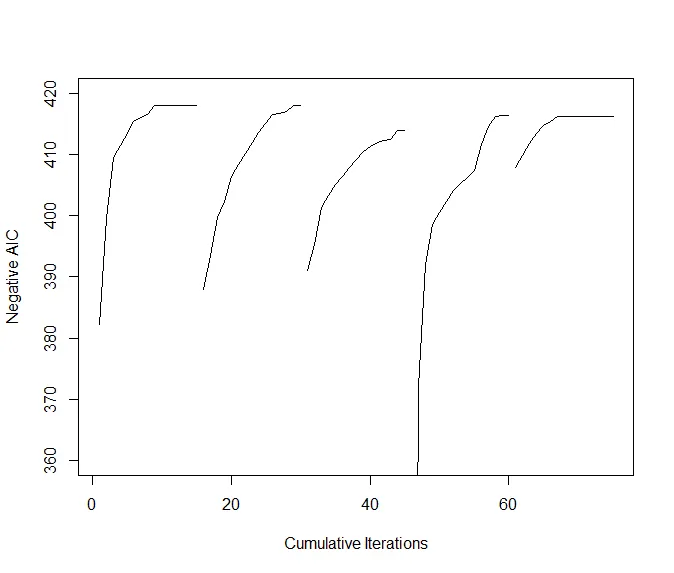
##Iteration에 따른 AIC 변화
plot(1:(itr*num.starts),-c(t(runs.aic)),xlab="Cumulative Iterations",
  ylab="Negative AIC",ylim=c(360,420),type="n")
for(i in 1:num.starts) {
  lines((i-1)*itr+(1:itr),-runs.aic[i,]) }
R
복사

2) First-Choice Climbing

#setting은 위와 동일
runs2 = matrix(0,num.starts,m)
runs.aic2 = matrix(0,num.starts,itr)

# INITIALIZES STARTING RUNS
set.seed(1234) 
for(i in 1:num.starts){runs2[i,] = rbinom(m,1,.5)} 
#random으로 열을 뽑는 것을 다섯 번 시행

for(k in 1:num.starts){
  run.current = runs2[k,]
  
  # ITERATES EACH RANDOM START
  for(j in 1:itr){
    run.vars = baseball.sub[,run.current==1] #1로 선택된 변수들 뽑아내기.
    g = lm(salary.log~.,run.vars)
    run.aic = extractAIC(g)[2] #[1]은 equivalent d.f, [2]가 AIC
    run.next = run.current
    
    #aic가 작은게 나오면 바로 채택
    for(i in 1:m){
      run.step = run.current
      run.step[i] = !run.current[i] #0이라면 1로 1이라면 0으로 바꿈.
      run.vars = baseball.sub[,run.step==1] #바뀐 것으로 variable을 새로 뽑음.
      g = lm(salary.log~.,run.vars) #model 적용
      run.step.aic = extractAIC(g)[2] #AIC 구하기
      if(run.step.aic < run.aic){
        run.next = run.step
        run.aic = run.step.aic
        break
      } #만약 AIC가 더 작다면 run.next로 할당해줌. 그리고 run.aic도 바꿔줌
    }
    run.current = run.next #run.next를 current에 적용.
    runs.aic2[k,j]=run.aic 
  }
  runs2[k,] = run.current #최종적으로 제일 작은 aic를 가진 subset이 골라짐.
}

runs2
runs.aic2
R
복사

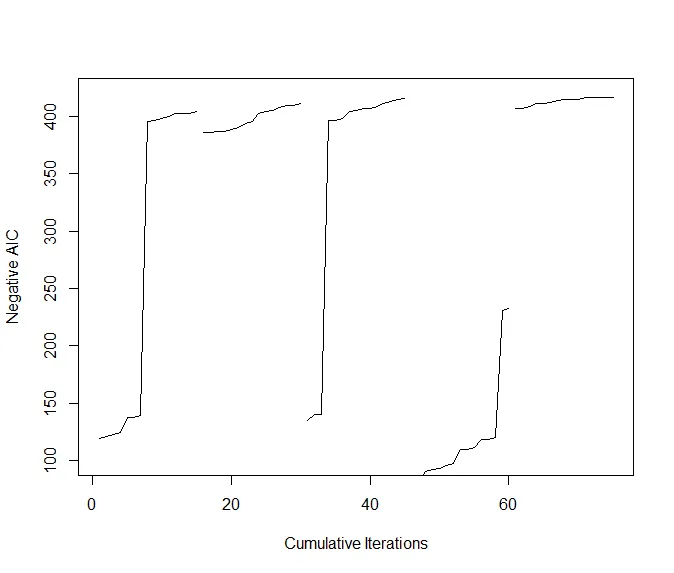
##Iteration에 따른 AIC 변화
plot(1:(itr*num.starts),-c(t(runs.aic2)),xlab="Cumulative Iterations",
     ylab="Negative AIC",ylim=c(100,420),type="n")
for(i in 1:num.starts) {
  lines((i-1)*itr+(1:itr),-runs.aic2[i,]) }
R
복사

→ Steepest 방식에 비해서 결과가 급격히 변하는 모습을 볼 수 있다.